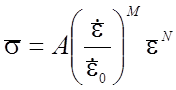Машиностроение \ Теоретические основы технологии производства деталей и сборки машин

Современное состояние и тенденции развития моделирования процессов механической обработки, страница 16

,                                                                  (2)

где ; М = 0,018+0,000038Т; A = 910exp(-0,0011T)+120exp(-0,00004(T-280)2)+ 50exp(-0,00001(T-600)2), N=0,16exp(0,0017T)+0,09exp(-0,00003(T-370)2)

Трение на передней поверхности измерялось методом разрезного резца (split tool method) [102]. Результаты, представленные на рис. 9 [КДВ71] при малых нормальных напряжениях могут быть описаны кулоновским законом трения с m = 1,0. При больших нормальных давлениях касательные напряжения ассимптотически приближаются к 360 МПа, что составляет 0.82 от величины касательных напряжений в плоскости сдвига зоны первичных деформаций. Как данные по пределу текучести так и по трению были получены Т. Китагавой (T. Kitagawa), работающего в технологическом институте Китами (Kitami Institute of Technology). Кроме того, исходными данными для моделирования являлись теплопроводность инструментального материала, равная 46 Вт/(м×К), а также теплопроводность и удельная массовая теплоемкость обрабатываемого материала, равная соответственно 62-0,044Т Вт/(м×К) и 450+0,38Т Дж/(кг×К).

 Участники этой круговой системы использовали ряд конечно-элементных методик. Выделенные в скобках числа соотвествуют нумерации на рис. 7. Упруго-пластическое моделирование было выполнено МИС {Обикава – Токийский технологический институт (Obikawa – Tokyo Institute of Technology) (1), Чайлдc – университет города Лидс (Childs – Leeds University) (2)} и нестационарным методом {Уида - Университет города Кобе (Ueda – Kobe University) (3)}. Другие три исследователя использовали один и тот же алгоритм (програмный код) адаптивного построения КЭ сетки для случая  жестко-пластического материала {Элтан – государственный университет Огайо (Altan – Ohio State University) (1), Барселона – университет Палермо (Barcelona – Palermo University) (2), Серетти – университет Брескиа (Ceretti – Brescia University) (4,5)} в то время как два других использовали другие методы для случая жестко-пластического материала {Уида (3) и Леополд – Чемнитс (Leopold – Chemnitz) (6)}. На рисунках  с 7,а по 7,г представлены результаты сравнения расчетных данных с экспериментом. Расчетные значения Fc и FT (рис. 7,а) располагаются вокруг их экспериментальных значений с большим разбросом величин Fc , чем FT и малым различием между результатами, полученными упруго- и жестко-пластическими методами. Средний коэффициент трения равен Fc /FT = 0,5. Расчетные значения длины контакта (рис. 7,б) и угла сдвига сильно различаются при решении упруго- и жестко-пластическими методами. Упруго-пластические методы дают большую длину контакта и меньший углы сдвига, близкие к действительности. Жестко-пластические методы также показывают довольно большую изменчивость в прогнозировании контактной температуры на передней поверхности (рис. 7,в), чем упруго-пластические методы, которые также дают результаты близкие к экспериментальным.

По результатам расчетом может быть выполнена проверка непротиворечивости результатов. Частное от деления результирующей силы резания приведенной к плоскости сдвига к площади этой плоскости является касательными напряженийями течения в зоне перыичных деформаций. В табл. 1 приведены экспериментально измеренные значения этих напряжаний (их величина, рассчитанная из уравнения 1, составляет 480-510 МПа в зависимости[КДВ72]  от принятых допущений о влиянии деформаций и температуры). Многоие модели дают результаты по величине большие указанной.

Вторая проверка заключается в сравнении с нормальными напряжениями наблюдаемого режима трения (friction behavior) на передней поверхности при изменении коэффициента трения (friction) (рис. 7,г)[КДВ73] . Большинство результатов расчета (но не все) указывают на трение в области малых и больших величин нормальных напряжений, и практически не наблюдаются трение в области средних величин нормальных напряжений.

Таблица 1. Измеренные и вычисленные касательные напряжения в зоне первичных деформаций (МПа)

Эксперимент

Упругопластическая модель

Жестко-пластическая модель

1

2

3

1

2

4

5

6

445

635

485

551

792

570

737

724

490

Рис. 7 показывает, что некоторые методы КЭ могут прогнозировать условия обработки. Объяснение результатов табл. 1 заключается в том, что много пакетов программ в настоящее время имеют трудности в управлении внутренним равновесием, возможно компоненты гидрастатических давлений. Задание по круговой системе показало, что это является важным вопросом. Было также показано, что моделирования трения является областью, где необходимы дополнитеьные исследования: средний коэффициент трения величиной 0,5 в приведенном примере скрывает свое изменение от 1,0 до условий, когда касательные напряжения (трения) не зависят от нормальных напряжений. Конечно, к полученным данным по величине предела текучести при больших величинах деформаций, скоростей деформаций и температур также необходимо относиться с осторожностью.

Рис. 7 Экспериментальные (+) и расчетные (жестко-пластическая модель , упруго-пластическая модель ) изменения Fc c FT (а), lc c f/tan(F) (б), распределения температуры вдоль передней поверхности (с) и касательных напряжений трения с  изменением нормальных напряжений на передней поверхности.

4.4 Современные достижения в вычислительной механике резания и некоторые ее трудности

4.4.1 Основное уравнения резания металлов

Главной целью исследований в области обработки металлов резанием является разработка аналитических систем позволившие бы нам прогнозировать показатели процесса резания без проведения экспериментов, что необходимо для назначения режимов резания (условий обработки). Одна процессы резания являются очень сложными со множеством взаимосвязанных явлений (рис. 8).

Скачать файл