Validation for the Cox Model. Terry M. Therneau Mayo Foundation. Breslow estimates. Exact partial likelihood, страница 9

The hazard increment and mean at times 1 and 4 are identical to those for the Breslow approximation, as shown in table 3. At time 2, the number at risk for the first, second and third portions of the hazard increment are n₁ = 11r + 5, n₂ = (2/3)(7r + 3) + 4r + 2 = (26r + 12)/3, and n₃ = (1/3)(7r + 3) + 4r + 2 = (19r + 9)/3. Subjects F–I experience the full hazard at time 2 of (10/3)(1/n₁ + 1/n₂ + 1/n₃), subjects B–D experience (10/3)(1/n₁ + 2/3n₂ + 1/3n₃). Thus, at β = 0 the martingale residuals are

The hazard estimate for a hypothetical subject with covariate X^† is Λ_i(t) = exp(X^†β)Λ₀(t), Λ₀ has increments of 1/(r²+11r+7, (10/3)(1/n₁+ 1/n₂ + 1/n₃) and 2/(2r + 1). This increment at time 2 is a little larger than the Breslow jump of 10/d1. The first term of the variance will have an increment of [exp(() at time 2. The

increment to the cumulative distance from the center d will be

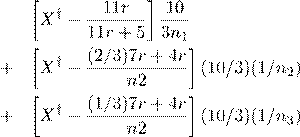
For X^† = 1 and β = π/3 we get cumulative hazard and variance below.

We have r = e^π/3,

                                      Λ                                 Variance

           e/(r² + 11r + 7)     0.03272832      e²/(r² + 11r + 7)²

4  Test data 4

This is an extension of test data set 3, but with 3 covariates. Let r_i = exp(X_β) be the risk score for each subject, β unspecified. Table 4 shows the data set along with the mean and increment to the hazard at each point.

At β = 0 we have r = 1 and

/d

Table 4: Test data 4