Validation for the Cox Model. Terry M. Therneau Mayo Foundation. Breslow estimates. Exact partial likelihood, страница 3

The variance formula for the baseline hazard function is extended in the same way, and is the sum of (hazard increment)², treating a tied death as d separate hazard increments. In term 1 of the variance, the increment at time 6 is now 1/(r +3)² +4/(r +5)² rather than 2/(r +3)². The increment to d at time 6 is (r/(r+3))∗1/(r+3)+(r/(r+5))∗2/(r+5). (Numerically, the result of this computation is intermediate between the Nelson–Aalen variance and the Greenwood variance used in the Kaplan–Meier, which is an increment of

 .

The denominator for the Greenwood formula is the sum over those at risk, times that sum without the deaths. At time 6 this latter is 2/[(r + 3)(3)].) For β = 0, x = 0, let v = I⁻¹ = 144/83.

For β = 1.676857, x = 0.

Given the cumulative hazard, the martingale and score residuals follow directly using similar computations. Subject 3, for instance, experiences a total hazard of 1/(3r + 3) at the first death time, 1/(r + 3) at the “first” death on day 6, and (1/2) ∗ 2/(r + 5) at the “second” death on day 6 — notice the case weight of 1/2 on the last term. Subjects 5 and 6 experience the full hazard of 1/(r+3)+2/(r+5) on day 6. The values of the martingale residuals are as follows.

Let a = r + 1, b = r + 3, and c = r + 5; then the score residuals are

For subject 3, the score residual was computed as

 ;

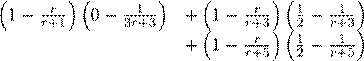the single death is counted as 1/2 event for each of the two day 6 events. Another equivalent approach is to actually form a second data set in which subjects 3 and 4 are each represented by two observations, one at time 6 and the other at time 6+, each with a case weight of 1/2. Then a computation using the Breslow approximation will give this score residual as the weighted sum of the score residuals for the two psuedo-observations.

The Schoenfeld residuals for the first and last events are identical to the Breslow estimates, that is, 1/(r + 1) and 0, respectively. The residuals for time 6 are 1 − c and 0 − c, where c = (1/2){r/(r + 3) + r/(r + 5)}, the

“average” ¯x over the deaths.

It is quite possible to combine the Efron approximation for β^ˆ along with the Breslow (or Nelson–Aalen) estimate of Λ, and in fact this is the behaviorˆ used in some packages. That is, if the ties=efron option is chosen the formulas for LL, U, and I are those shown in this section, while the hazard and residuals all use the formulas of the prior section. Although this is not perfectly consistent the numerical effect on the residuals is minor, and it does not appear to affect their utility. S uses the calculations of this section by default.