|
Breslow |
Efron |
|||||||||||
|
LL |
|
|
+ |
|
||||||||
|
U |
2 3r+2 |
1 3r+2 |
+ |
1 2r+2 |
||||||||
|
I |
|
|
+ |
|
||||||||
|
dΛˆ |
2 3r+2 |
1 3r+2 |
+ |
1 2r+2 |
||||||||
|
Time |
Status |
X |
Wt |
x¯(t) |
dΛˆ0(t) |
|||||||
|
1 |
1 |
2 |
1 |
(2r2 + 11r)dΛˆ0 = ¯x1 |
1/(r2 + 11r + 7) |
|||||||
|
1 |
0 |
0 |
2 |
|||||||||
|
2 |
1 |
1 |
3 |
11r/(11r + 5) = ¯x2 |
10/(11r + 5) |
|||||||
|
2 |
1 |
1 |
4 |
|||||||||
|
2 |
1 |
0 |
3 |
|||||||||
|
2 |
0 |
1 |
2 |
|||||||||
|
3 |
0 |
0 |
1 |
|||||||||
|
4 |
1 |
1 |
2 |
2r/(2r + 1) = ¯x3 |
2/(2r + 1) |
|||||||
|
5 |
0 |
0 |
1 |
|||||||||
Table 3: Test data 3
This is very similar to test data 1, but with the addition of case weights. There are 9 observations, x is a 0/1/2 covariate, and weights range from 1 to 4. As before, let r = exp(β) be the risk score for a subject with x = 1. Table 3 shows the data set along with the mean and increment to the hazard at each point.
The likelihood is now a product of terms, one for each death, of the form
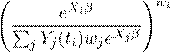
leading to a log-likelihood very like equation ??
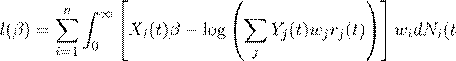 ) (1)
) (1)
For integer weights, this gives the same results as would be obtained by replicating each observation the specified number of times, which was in fact one motivation for the definition. The definitions for the score vector U and information matrix I simply replace the mean and variance with weighted versions of the same. Let l(β,w) be the logliklihood when all the observations are given a common case weight of w; it is easy to prove that l(β,w) = wl(β,1) − dlog(w) where d is the number of events. One consequence of this is that the log-likelihood can be positive when many of the weights are < 1, which sometimes occurs in survey sampling applications. (This can be a big surprise the first time one encounters the situation.)
|
LL |
= |
{2β − log(r2 + 11r + 7)} + 3{β − log(11r + 5)} +4{β − log(11r + 5)} + 3{0 − log(11r + 5)} +2{β − log(2r + 1)} |
|
= |
11β − log(r2 + 11r + 7) − 10log(11r + 5) − 2log(2r + 1) |
|
|
U |
= |
(2 − x¯1) + 3(0 − x¯2) + 4(1 − x¯2) + 3(1 − x¯2) + 2(1 − x¯3) |
|
= |
11 − (¯x1 + 10¯x2 + 2¯x3) |
|
|
I |
= |
|
The solution corresponds to U(β) = 0, which is the solution point of the polynomial 66r4+425r3−771r2−1257r−385 = 0, or βˆ ≈ log(2.3621151) = 0.8595574. Then
|
LL(0) = −32.86775 |
LL(βˆ) = −32.02105 |
|
U(0) = 2.107456 |
U(βˆ) = 0 |
|
I(0) = 2.914212 |
I(βˆ) = 1.966563 |
When β = 0, the three unique values for ¯x at t = 1, 2, and 4 are 13/19, 11/16 and 2/3, respectively, and the increments to the cumulative hazard are 1/19, 10/16 = 5/8, and 2/3, see table 3. The martingale and score residuals at β = 0 are βˆ of
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.