Validation for the Cox Model. Terry M. Therneau Mayo Foundation. Breslow estimates. Exact partial likelihood, страница 5

Table 2: Test data 2

2  Test data 2

This data set also has a single covariate, but in this case a (start, stop] style of input is employed. Table 2 shows the data sorted by the end time of the risk intervals. The columns for ¯x and hazard are the values at the event times; events occur at the end of each interval for which status = 1.

2.1  Breslow approximation

For the Breslow approximation we have

.

.

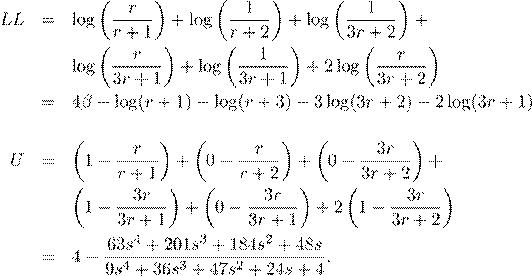The solution is at U(β^ˆ) = 0 or r ≈ .9189477; β^ˆ = log(r) ≈ −.084529.

Then

                                   LL(0) = −9.392662      LL(β^ˆ) = −9.387015

                                   U(0) = −2/15                 U(β^ˆ) = 0

                                  I(0) = 2821/1800         I(β^ˆ) = 1.586935.

The martingale residuals are (status–cumulative hazard) or O−E = δ_i− ^R Y_i(s)r_idΛ(^ˆ s). Let λ^ˆ₁,...,λ^ˆ₆ be the six increments to the cumulative hazard listed in Table 2. Then the cumulative hazards and martingale residuals for the subjects are as follows.

The score and Schoenfeld residuals can be laid out in a tabular fashion.

Each entry in the table is the value of) for subject i and event time t_j. The row sums of the table are the score residuals for the subject; the column sums are the Schoenfeld residuals at each event time. Below is the table for β = log(2) (r = 2). This is a slightly more stringent test than the table for β = 0, since in this latter case a program could be missing a factor of r = exp(β) = 1 and give the correct answer. However, the results are much more compact than those for β^ˆ, since the solutions are exact fractions.

Both the Schoenfeld and score residuals sum to the score statistic U(β). As discussed further above, programs will return two Schoenfeld residuals at time 7, one for each subject who had an event at that time.

2.2  Efron approximation

This example has only one tied death time, so only the term(s) for the event at time 9 change. The main quantities at that time point are as follows.