Validation for the Cox Model. Terry M. Therneau Mayo Foundation. Breslow estimates. Exact partial likelihood, страница 2

The second term is dI⁻¹d⁰, where I is the variance–covariance matrix of the Cox model, and d is a vector. The second term accounts for the fact that the weights themselves have a variance; d is the derivative of S(t) with respect to β and can be formally written as

.

This can be recognized as −1 times the score residual process for a subject with x_i as covariates and no events; it measures leverage of a particular observation on the estimate of β. It is intuitive that a small score residual — an obs with such covariates has little influence on β — results in a small added variance; that is, β has little influence on the estimated survival.

For β = 0, x = 0:

For β = 1.4752849, x = 0

1.2  Efron approximation

The Efron approximation [?] differs from the Breslow only at day 6, where two deaths occur. A useful way to think about the approximation is this: assume that if the data had been measured with higher accuracy that the deaths would not have been tied, that is two cases died on day 6 but they did not perish at the same instant on that day. There are thus two separate events on day 6. Four subjects were alive and at risk for the first of the events. Three subjects were at risk for the second event, either subjects 3, 5, and 6 or subjects 2, 5, and 6, but we do not know which. In some sense then, subjects 3 and 4 each have “.5” probability of being at risk for the second event at time 2 + . In the computation, we treat the two deaths as two separate times (two terms in the loglik), with subjects 3 and 4 each having a case weight of 1/2 for the second event. The mean covariate for the second event is then

and the main quantities are

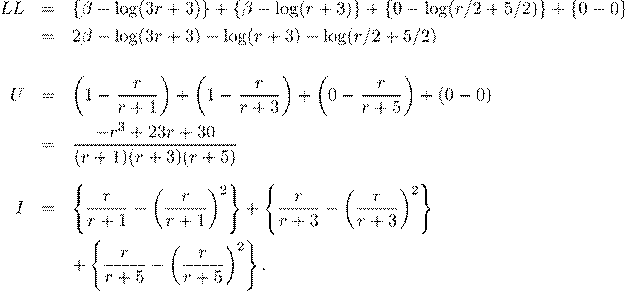
The solution corresponds to the one positive root of U(β) = 0, which can

be written as φ = arccos{(45/23)^p3/23}, r = 2^p23/3cos(φ/3) ≈ 5.348721, or β^ˆ = log(r) ≈ 1.676858. Then

The cumulative hazard now has a jump of size 1/(r + 3) + 2/(r + 5) at time 6. Efron [?] did not discuss estimation of the cumulative hazard, but it follows directly from the same argument as that used for the loglikelihood so we refer to it as the “Efron” estimate of the hazard. In S this hazard is the default whenever the Efron approximation for ties is used; the estimate is not available in SAS. For simple survival curves (i.e., the no-covariate case), the estimate is explored by Fleming and Harrington [?] as an alternative to the Kaplan–Meier.