![]()
![]()
![]()
![]()
![]()
![]()
![]()
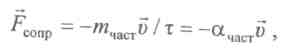
где ![]() - коэффициент пропорциональности (при переходе
от отдельной частицы к единице ее объема
заменяем
- коэффициент пропорциональности (при переходе
от отдельной частицы к единице ее объема
заменяем![]() на
на![]() ).
).
В нестесненных условиях, когда сепарируемые минеральные частицы «одиноко», не взаимодействуя друг с другом, движутся сквозь однородную среду типа воды или воздуха, силы градиентная и сопротивления пропадают (сопротивление среды остается).
Рассмотрим диффузионные
эффекты совместного действия градиентной
силы и силы сопротивления. Если на частицы элементарной фракции ![]() действуют
только две силы
действуют
только две силы![]() и
и
![]() то
частицы ведут себя в зоне сепарации, как при свободной диффузии. Для доказательства возьмем за исходные
уравнения сохранения (4) и (8) при
то
частицы ведут себя в зоне сепарации, как при свободной диффузии. Для доказательства возьмем за исходные
уравнения сохранения (4) и (8) при ![]() и уравнения баланса сил:
и уравнения баланса сил:
|
|
|
|
(9)
Исключив ![]() с помощью подстановки
получим уравнение диффузии для функции состояния
с помощью подстановки
получим уравнение диффузии для функции состояния ![]()
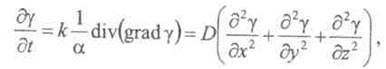 (10)
(10)
![]()
![]() где введен коэффициент
макродиффузии
где введен коэффициент
макродиффузии ![]() м2/с
.
м2/с
.
Обозначим концентрацию
элементарной ![]() -й
фракции при
-й
фракции при ![]() через
через ![]() ,
тогда уравнение примет вид
,
тогда уравнение примет вид
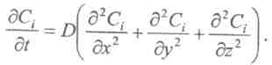
Таким образом, получили
традиционное уравнение диффузии, но нетрадиционным путем, взяв в качестве
первопричины не законы Фика, а только две силы ![]() и
и ![]() Математические решения
уравнения диффузии и практика свободной диффузии показывают стремление частиц равномерно распределиться по пространству,
не концентрироваться и не сепарироваться.
Математические решения
уравнения диффузии и практика свободной диффузии показывают стремление частиц равномерно распределиться по пространству,
не концентрироваться и не сепарироваться.
Силы типа архимедовой являются другой группой нетрадиционных сил, принимающих участие в сепарационных процессах.
Ускорительно-архимедова
сила возникает
в обогатительных аппаратах, где
частицы и среда движутся с ускорением ![]() и
появляется сила реакции границ рабочей зоны
и
появляется сила реакции границ рабочей зоны
![]() (11)
(11)
Центробежно-архимедова сила возникает в гидроциклонах, винтовых сепараторах и подобных аппаратах с круговым движением среды и частиц, где
![]() (12)
(12)
где ![]()
Магнитно-архимедова сила возникает в магнитных суспензиях или пульпах
с магнитными частицами в рабочих зонах, помещенных в магнитное поле ![]()
![]() (13)
(13)
В рабочих зонах сепараторов возможны и другие силы типа архимедовой.
Методика составления уравнений
сепарации в рабочих зонах включает объединение уравнений закона сохранения и
баланса сил, специфичных
для различных обогатительных аппаратов. Рассмотрим методику на типичном примере одномерной ![]() рабочей
зоны отсадочной машины. Два совокупных исходных уравнения имеют вид
рабочей
зоны отсадочной машины. Два совокупных исходных уравнения имеют вид
|
|
Подставляя скорость![]() из
второго уравнения (14) в первое, получим одно уравнение сепарации, которое
содержит только одну неизвестную функцию
из
второго уравнения (14) в первое, получим одно уравнение сепарации, которое
содержит только одну неизвестную функцию![]() решения уравнения сепарации
предсказывают фракционный состав в зоне. Наоборот, подставляя функцию
решения уравнения сепарации
предсказывают фракционный состав в зоне. Наоборот, подставляя функцию ![]() из одного уравнения в другое (14), получим одно уравнение для
поля скоростей, которое содержит только
одну неизвестную функцию
из одного уравнения в другое (14), получим одно уравнение для
поля скоростей, которое содержит только
одну неизвестную функцию![]() для предсказания сепарационных
скоростей частиц в зоне.
для предсказания сепарационных
скоростей частиц в зоне.
В частном случае, для отсадочной машины с естественной постелью, получим следующее уравнение сепарации:
|
|
где ![]() - коэффициент макродиффузии, м2/с.
- коэффициент макродиффузии, м2/с.
Для других аппаратов получаются другие конкретные уравнения сепарации.
Математические решения
уравнений сепарации предсказывают картину
движения минеральных фракций в рабочих зонах, т.е. фракционный состав ![]() -
при заданных краевых (начальных и
граничных) условиях.
-
при заданных краевых (начальных и
граничных) условиях.
1. Тихонов О. Н. Закономерности эффективного разделения минералов в процессах обогащения полезных ископаемых. Л.: Недра, 1984. 200с.
2. Тихонов О. Н. Теория сепарационных процессов. Часть 1. СПб. 2004.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.