Общие закономерности движения минеральных частиц в рабочих зонах обогатительных аппаратов. Взаимосвязь между полем скоростей и функцией состояния в виде закона сохранения, страница 5

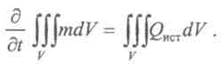
В упомянутом частном случае сосредоточенияв трех точках

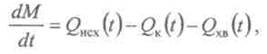
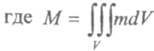 - суммарное количество минерального материала, запасенного в зоне, кг или м³.

В качестве примера рассмотрим постель отсадочной машины (см. рис.1). Здесь достаточно одномерной задачи, так как сепарация проходит в вертикальном направлении х между границами . Продвижение минерала от загрузки к разгрузке со скоростью транспортировки можно заменить временем . Функцией состояния является В этом случае интегральный закон (7) принимает вид

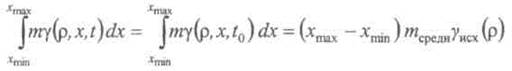
и показывает зависимость между фракционным составом исходного материалаи функцией состояния

4. Силы, действующие на минеральные частицы

Для предсказания функций состояния недостаточно знать закон сохранения, так как он выражается одним уравнением с двумя неизвестными . Чтобы получить два уравнения с двумя неизвестными, необходимо еще одно соотношение между . Перейдем к нахождению этого соотношения или, точнее говоря, соотношений, так как для различных обогатительных аппаратов оно будет отличаться. Необходимо найти такое соотношение, которое может оценить векторное поле  скоростей частиц.

Для получения этих соотношений можно применять различные законы физики. Для единообразия, простоты и наглядности в качестве основного соотношения возьмем уравнение баланса статистически усредненных сил, действующих на частицы любой элементарной фракции, которое запишем для начала в нерасшифрованном виде:

                                                            (8)

т.е. сумма сил, действующих на частицу (или на единицу объема элементарной фракции ), равна нулю.

Равенство (8) связано с законом сохранения импульса (количества движения): сумма сил (внешних и взаимодействия), действующих на группу частиц любой элементарной фракции , равна скорости изменения полного импульса всех этих частиц. В равенстве (8) допускается, что упомянутый полный импульс не изменяется (хотя из-за случайных движений импульсы отдельных частиц изменяются).

Уравнение типа (8) является вторым и последним (после закона   сохранения)   условием   нахождения   функций и оно содержит две эти функции и вместе с законом сохранения позволяет получать два уравнения с двумя неизвестными. В отличие от универсального закона сохранения уравнение баланса сил специфично для каждого аппарата; закон сохранения абсолютно точен, уравнение баланса сил всегда приближенно, степень точности его зависит от правильности выбора главных сил для данного аппарата.

Рассмотрим различные силы , действующие в обогатительных аппаратах. Их классифицируют на традиционные детерминированные и нетрадиционные среднестатистические. Можно группировать также по виду процессов обогащения, в которых они встречаются: силы в гравитационном обогащении, силы в магнитном обогащении и т.д. Поскольку одни и те же силы, например сила гравитации, часто встречаются в различных процессах, вначале рассмотрим природу отдельных сил. Все силы будем измерять в ньютонах на кубический метр, т.е. относить их действие к единице объема минеральных частиц.

Гравитационная сила, отнесенная к единице объема частицы с плотностью, определяется по формуле

Сила Архимеда в однородной среде (вода, суспензия) с плотностью - по формуле

Силыважны в гравитационных обогатительных аппаратах (отсадочных машинах, суспензионных сепараторах), когда сепарация основана на различии плотностей частиц.

Сила Стокса в однородной среде (воздух, вода, суспензия) определяется по формуле

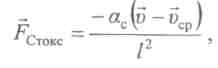
где- коэффициент сопротивления, пропорциональный вязкости среды, при шарообразной форме частиц - коэффициент динамической вязкости среды; и- скорость соответственно частицы и среды, м/с; / - (гидравлический) размер частицы, м.

Сила имеет большое значение при сепарации в сгустителях и классификаторах частиц, отличающихся крупностью l.