Общие закономерности движения минеральных частиц в рабочих зонах обогатительных аппаратов. Взаимосвязь между полем скоростей и функцией состояния в виде закона сохранения, страница 4

Из уравнения (5) следует условие постоянства в виде ^.

До сих пор мы рассматривали законы сохранения без учета источников (или стоков) материала внутри зоны. Однако такие источники могут иметь место, причем они могут быть или распределены по пространству, части пространства или сосредоточены в точке, плоскости, на линии, поверхности.

Подвод и отвод удобно количественно характеризовать производительностью источника по любой элементарной фракции на единицу объема пространства:

где - суммарный поток всех фракций, кг/(м³с) или м³/(м³-с);

 - распределение этого потока по фракциям,

Функция не эквивалентна функции состояния , характеризующей материальный состав зоны аппарата. В фундаментальной задаче предсказания массопереносаобычно является заданной (например, характеризует фракционный состав исходного питания).

Рассмотрим в качестве примера сосредоточенного источника точечный источник. Такие источники практически не существуют, и понятие о точечном источнике является упрощением, при котором небольшая часть пространства, где материал вводится (отводится), умышленно стягивается в точку, что позволяет упростить математические операции. Если точечный источник расположен вточке зоны, то для него функцию производительности можно записать в виде

 - полная производительность источника, кг/с или м³/с;-дельта-функция, указывающая местоположение источника, 1/м³.

Таким образом, если материал вводится в зону в точке, то его можно охарактеризовать двумя простыми (по сравнению с общим случаем) функциями - суммарной производительностью и фракционным составом ^.

Чтобы сосредоточить (стянуть) распределенный по объему источник в точку, расположенную внутри объема надо из функций , заданных в этом объеме, найти

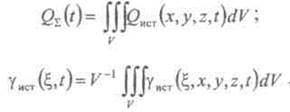
Этим путем все распределенные источники можно сосредоточить в одной точке или нескольких.

Важный для практики случай: в одну точку стягивается подвод исходного питания аппарата , в другие точки - отвод концентратаи хвостов ; причем соответствующие -функции указывают координаты этих точек. Тогда для равенства (4) производительность всех потоков можно объединить в виде ^.

Аналогичные рассуждения имеют место, когда сосредоточивание производится не в точку, а на линию или поверхность.

Для стационарного режима локальные законы (4)

и (5) принимают вид

Интегральный закон сохранения для зоны сепарации. Интегрирование полокального закона сохранения по объему Vвсей зоны сепарации дает следующий интегральный закон сохранения для элементарной фракции:

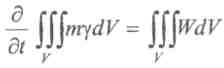                        (6)

Объемный интеграл от равен нулю, так как, во-

первых, на границах зоны скорость

и, во-вторых, в соответствии с теоремой Остроградского - Гаусса

Посколькуи на поверхностиограничивающей объем зоны , левый интеграл по поверхности, а следовательно, и правый по объему равны нулю.

В частном случае, если производительностьсосредоточена в точках подвода питания и отвода концентрата и хвостов, интегральный закон (6) принимает вид

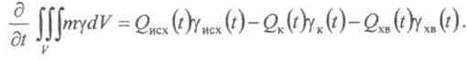
Физический смысл интегрального закона следующий: секундное изменение суммарного количества любой фракции, запасенной в зоне, равно разности потоков этой фракции, подводимых с исходным питанием и отводимых с концентратом и хвостами.

При  отсутствии  источников интегральный  закон имеет вид

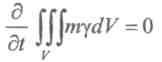
или после преобразований

(7)

где Vи М- соответственно полный объем и запас материала в зоне; - соответственно средние степень заполнения и фракционный состав.

В этом случае физический смысл интегрального закона следующий: средний фракционный состав в зоне без источников (и стоков) не меняется с течением времени.

Аналогично интегрирование по локального закона (5) дает интегральный закон сохранения для всего материала: