Общие закономерности движения минеральных частиц в рабочих зонах обогатительных аппаратов. Взаимосвязь между полем скоростей и функцией состояния в виде закона сохранения, страница 3

2. Понятие о поле статистических усредненных скоростей движения частиц элементарных фракций в зоне

Взоне сепарации аппарата под действием приложенных сил минеральные частицы любой элементарной фракции движутся с усредненной скоростью , зависящей от :

 - единичные векторы вдоль осей координат  Здесь вектор скорости разложен на составляющие вдоль осей координат. Усредненная скорость - это такая скорость, из которой исключена хаотическая случайная составляющая.

Векторная функция  для во всех точках зоны сепарации определяет поле скоростей элементарной фракции . Поля скоростей различных фракций различны, поэтому одни фракции движутся к разгрузке концентрата , а другие – к разгрузке хвостов . Объединенное поле скоростей всех фракций в диапазоне определяется функцией при переменном ^.

Нахождение поля скоростей является важнейшим промежуточным шагом в решении поставленной выше фундаментальной задачи предсказания: по известной функции однозначно и строго вычисляется и предсказывается искомая функция состояния ^.

3. Взаимосвязь между полем скоростей и функцией состояния в виде закона сохранения

Локальный закон сохранения для элементарной фракции. Между функциями и существует взаимосвязь, называемая законом сохранения.

Физический смысл закона (а также его следствий и разновидностей) можно выразить следующей словесной формулой:

Секундное накопление материала в произвольном объеме =

= Входящий через границу поток - Выходящий через границу поток +

+ Поток источника внутри объема.

Локальный фракционный, т.е. справедливый для окрестности любой локальной точки (х,у,г) и любой элементарной фракции, закон сохранения может быть записан в следующем виде:

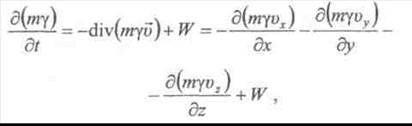                        (4)

где      или же в общем случае - подводимы (отводимый) поток источника (стока) фракций.

Напомним, что дивергенцией любой векторной функции  зависящей от    (здесь или  ), является скалярная функция

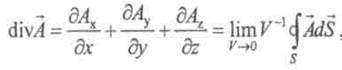
где   -  проекции   на соответствующие оси ; - локальный  объем;   -  ограничивающая  поверхность  вокруг  точки ()

При вместо уравнения (4) можно записать

Идея доказательства такова. Для элемента пространства (рис.2, а):

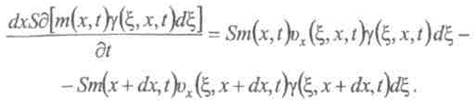
При нескольких физических свойствах и трехмерном пространстве идея вывода аналогична, но учитывается, что накопление частиц элементарной фракции происходит в произвольном элементе объема. В этом общем случае суммирование потоков элементарной фракции производится по замкнутой поверхности вокруг объема поэтому баланс «сумма потоков равна накоплению» имеет вид (аргументы функций опущены)

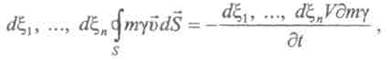
 - скалярное произведение, характеризующее поток, перпендикулярный к элементу поверхности(вектор направлен наружу нормально к и по значению равен ).

В соответствии с определением дивергенции левая часть преобразуется следующим образом:

и равенство выражает закон сохранения (4)

Рис.2. Накопление элементарной фракции в элементе одномерного (а) и трёхмерного (б) пространства

В распространенном на практике случае постоянной степени заполнения величина т в левой и правой частях уравнения (4) сокращается.

С точки зрения математики закон (4) представляет собой одно уравнение с двумя неизвестными функциями, поэтому его решение не позволяет определить функцию состояниядля конкретного обогатительного аппарата, т.е. решить фундаментальную задачу предсказания (и потребуется еще равенство с учетом сил, действующих на частицы).

Дополнительно, как следствие, отметим локальный закон сохранения для всей суммы фракций, получаемый интегрированием по  из уравнения (4):

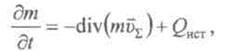                                   (5)

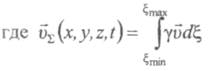 - средняя по фракциям скорость минеральных частиц, т.е. скорость транспортировки всей смеси в зоне;-суммарный поток частиц всех фракций источника.