Термодинамические характеристики малой капли в рамках метода функционала плотности, страница 5

Известно [11], что расклинивающее давление приводит к немонотонному поведению химическоллоидный                               м 2 кого потенциала конденсата в капле, характерному для гетерогенной нуклеации на смачиваемых ядрах конденсации. Для того чтобы проанализировать влияние неоднородности центральной области гомогенно зародившейся капли на химический потенциал ее молекул, сравним зависимости химического потенциала конденсата от числа молекул v в капле, одна из которых получена обращением зависимости найденной методом функционала плотности, а вторая дается классическим капиллярным приближением

џс*ар =                 (4.8)

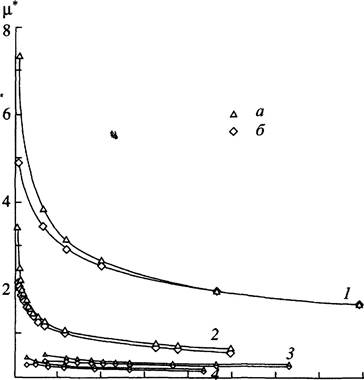
Напомним, что в (4.8) значения химического потенциала отсчитываются от , а Ль., — плотности однородной жидкости и пара при = . Результаты расчета зависимостей и џсар представлены на рис. 4 для двух значений температуры.

Видно, что в области малых значений v, порядка нескольких сотен частиц, расчетные кривые для и џс*ар расходятся. Обе кривые растут с уменьшением v, причем рост џс*ар превосходит и существенно рост џ*. Однако этот рост остается монотонным как для р * так и для

Таким образом, монотонная зависимость химического потенциала конденсата остается характерным признаком гомогенного механизма нуклеации даже с учетом существования неоднородности в центральной области капли. И попытка поправить теорию гомогенной нуклеации, базировавшаяся на возможности существования максимума на кривой химического потенциала конденсата в области малых размеров капель [15, 16], не находит основания в расчетах, выполненных методом функционала плотности.

Тот факт, что кривая проходит ниже кривой џс*ар  на понижение активационного барьера нуклеации как результат существования неоднородности в центральной области капли. Проиллюстрируем это понижение барьера с помощью кривой зависимости работы образования капли от ее размера. Пусть пересыщение пара задается значением химического потенциала, тогда работа образования критического зародыша, выраженная в единицах КБТ, имеет вид

                      (4.9)

Для определения зависимости работы образования капли от числа частиц в капле используем общее дифференциальное соотношение  =

61

0                    200                400                600                  800

Рис. 4. Зависимости химического потенциала от числа молекул v в капле: потенциал Юкавы. Т = 0.40Т (1); 0.80Тс (3); потенциал Леннард-Джонса. Т = 0.51 Тс (2); 0.80Тс (4). а — капиллярное приближение, б — метод функционала плотности.

= — џ* . Интегрируя это соотношение по переменной v, находим

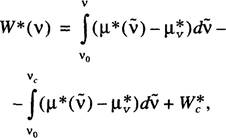            (4.10)

где vo — некоторая начальная точка на кривой  vc — размер критического зародыша при

Рассмотрим кривую            изображенную на рис. 4. Возьмем в качестве vo минимальное значение v на этой кривой. Полученные с помощью (4.10) результаты сравним с классической зависимостью Wc*ap (v), найденной в капиллярном приближении

(4.11)

Графики зависимостей W*(v) и Wc*ap (v) представлены на рис. 5. Видно, что максимум кривой (4.10) лежит ниже максимума кривой (4.11) (кривые построены при достаточно большом, но от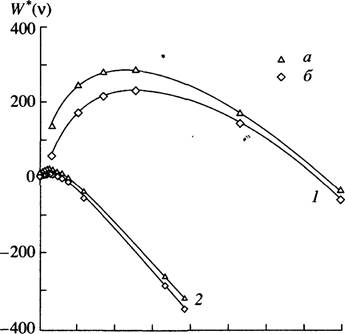

О          200          400          600         800

Рис. 5. Зависимость работы образования капли W*(v) от числа молекул v в капле: 1 — потенциал Юкавы. Т = 0.40Тс; 2 — потенциал Леннард-Джонса. Т = 0.51 Тс. а — капиллярное приближение; б — метод функционала плотности.

вечающем разумным высотам активационного барьера нуклеации значении что и означает понижение барьера нуклеации.

Заметим теперь, что неоднородность центрадьной области капли сказывается и на зависимости поверхностного натяжения б от размера капли. Эта проблема активно обсуждается в настоящее время в литературе [5—7], причем разными авторами используются различные определения поверхностного натяжения. Мы будем определять бе для введенной соотношением (4.2) эквимолекулярной поверхности радиуса Re

Q+pvV И- Ру

2(4.12)

где и ру — давления при заданном значении '.L в жидкой и газовой объемных фазах, соответственно.