Термодинамические характеристики малой капли в рамках метода функционала плотности, страница 2

Здесь Л(р) — плотность свободйой энергии системы жестких сфер, w(lr — r'l) — вклад в потенциал двухчастичного взаимодействия, связанный с притяжением частиц, — химический потенциал исследуемой системы, У — объем системы. ПредставляяЛ(р) в видеЛ(р) = рщ(р) —ph(p), где — химический потенциал, а — давление системы жестких сфер при заданных температуре Т и плотности p(r), для pth(p) и Ар) используем формулы Карнахана—Старлинга [9]

= КБТ[1пл + (811 —971 ² +             —Я) ³ ],

(2.2) Ph(p) = КБТр(1 + Л  —Я) ³ , где КБ — постоянная Больцмана, = пЮр/6 — безразмерная плотность, d — диаметр жесткой сферы.

Условие экстремальности Q[p(r)] в равновесии приводит к интегральному уравнению для равновесного профиля p(r):

(2.3)

61

В дальнейшем удобнее перейти к безразмерным радиусу-вектору и = r/d, плотности Л, давлению р* = (п/6)рЮ/КБТ, потенциалу взаимодействия w*(u) = химическим потенциалам  = џ/КБТи = џЏКБТ, большому термодинамиЧеСКОМУ потенциалу = ТКЁТ. В новых переменных уравнение (2.3) примет вид

(2.4)

Для объемных фаз интегральное уравнение (2.4) сводится к алгебраическому уравнению. Решая такое уравнение, находим критическую температуру Тс и для заданной температуры Т < Тс вы^т-шсляем значение химического потенциала РИТ), соответствующее равновесию жидкой и газовой фазы с плоской границей раздела между ними, а также значения плотностей и Лк, для жидкой и для газовой фаз, соответственно. Найденные значения Ь.џ, и служат опорными для последующего расчета профиля плотности в неоднородной капле.

З. МОДЕЛИ МЕЖМОЛЕКУЛЯРНОГО ПОТЕНЦИАЛА И АЛГОРИТМ

ВЫЧИСЛЕНИЙ

Для теории гомогенной нуклеации наибольший интерес представляет сферически симметричное решение уравнения (2.4), описывающее критический зародыш,т.к. его работа образования определяет высоту активационного барьера нуклеации. Но это решение (2.4) отвечает максимуму большого термодинамического потенциала и поэтому является неустойчивым, что порождает трудности при его нахождении.

Если имеет место сферическая симметрия, то тт(и) = п(и), тогда при V оо уравнение (2.4) в сферических координатах примет вид

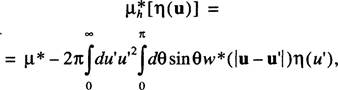 (3.1)

где lu—u'l = (и² + U'² —2uu'cos9)         (3.2)

е — азимутальный угол в системе координат, ось z в которой совпадает с направлением вектора и.

Интегрирование по углу е в уравнении (3.1) может быть проведено в аналитическом виде при выборе в качестве модели межмолекулярного взаимодействия потенциала Юкавы или ЛеннардДжонса в форме, предложенной Виксом, Чендлером и Андерсоном [10]. В размерных переменных потенциал Юкавы имеет вид

                       (3.3)

В выражении (3.3) имеется два параметра а и Х, которые могут быть определены независимо. Как показано в [2], параметр оказывает слабое влияние на свойства объемных фаз, но существенно влияет на свойства поверхностного слоя. Интересуясь более качественной, а не количественной стороной результатов расчетов с потенциалом Юкавы, положим, следуя [4], = 1/d. Окончательный вид уравнения (3.1) для потенциала Юкавы с учетом (3.2) и (3.3) будет тогда таков:

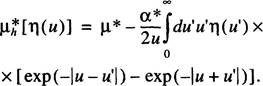          (3.4)

Более физически обоснованным является выбор в качестве модели межмолекулярного взаимодействия потенциала Леннард-Джонса в форме Викса, Чендлера, Андерсона [10]

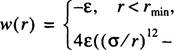(3.5) — (6/0 ⁶ ), r>rmin

где rmin —— 2 ¹/⁶6, е и б — параметры потенциала ЛенщТ+Ь

нард-Джонса. Следуя [З], положим d(7) = 0

(значения щ, ф, аз, Ь определены в [З]).Отметим

что кусочный характер функции (3.5) приводит при подстановке ее в (3.1) к очень громоздкому выражению, которое мы приводить не будем.

Рассмотрим процедуру решения уравнения (З. 1). Будем искать это решение итерационным способом, подставляя начальное приближение для п(и') в подынтегральное выражение в (3.1). Как показано в [2, З], такая процедура, вообще говоря, не является устойчиво сходящейся к решению, которое отвечает критическому зародышу, т.к. он находится в состоянии неустойчивого равновесия с паром. Поэтому, во-первых, необходимо подобрать хорошее начальное приближение, а во-вторых, выбрать критерий, согласно которому следует обрывать итерационный процесс в тот момент, когда результат наиболее близок к искомому профилю плотности в критическом зародыше.