где ру и р, — плотности объемных фаз, определяемые при химическом потенциале капли р. Из (4.1 ) вытекает следующее выражение для безразмерного радиуса R * эквимолекулярной разделяющей поверхности
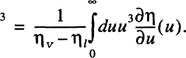 (4.2)
(4.2)
 0.2
0.2
10 20
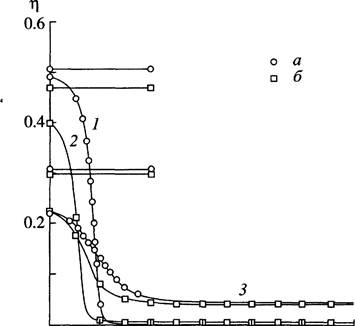
Рис. 1. Характерный вид профилей плотности п(и): Т = 0.40Тс (1); 0.51 Тс (2); 0.80Тс (З). Горизонтальные линии показывают значения плотности однородной жидкости при џ* = , а — потенциал Юкавы; б — потенциал Леннард-Джонса.
Под числом частиц в зародыше v будем понимать число частиц, находящихся внутри объема, ограниченного эквимолекулярной разделяющей поверхностью. В безразмерных переменных это число может быть записано в виде
![]() =
24Jduu Т И). (4.3)
=
24Jduu Т И). (4.3)
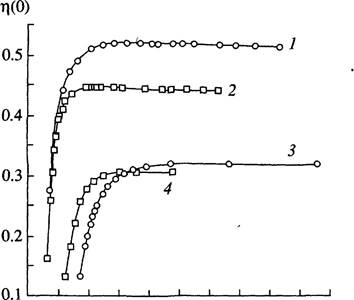
На рис. 2 представлена зависимость плотности числа частиц Л(О) в центре капли от радиуса R * эквимолекулярной поверхности. Отметим, что кривые, полученные для потенциалов Юкавы и Леннард-Джонса, похожи. Это указывает на то, что потенциал Юкавы дает качественно верное описание поведения малых систем в рамках метода функционала плотности.
Обращает на себя внимание немонотонный характер зависимости центральной плотности от размера капли. При убывании R * от больших значений величина ТО) сначала возрастает, как это предсказывается в рамках классической теории с учетом поправки на сжимаемость [12]. Однако при еще меньших плотность в центре капли резко убывает и становится меньше значения, соответствующего объемной жидкой фазе, демонстрируя эффект ”самоперекрытия” поверхностного слоя. Согласно рис. 2, эффект самоперекрытия проявляется при размерах капель,
61
0 5 10 15 20 25
Рис. 2. Зависимость плотности Л(О) в центре капли от радиуса R * эквимолекулярной разделяющей поверхности: потенциал Юкавы, Т = 0.40Тс (1); Т = 0.80Тс (З); потенциал Леннард-Джонса, Т = 0.51 Тс (2); Т = 0.80Тс (4).
![]()
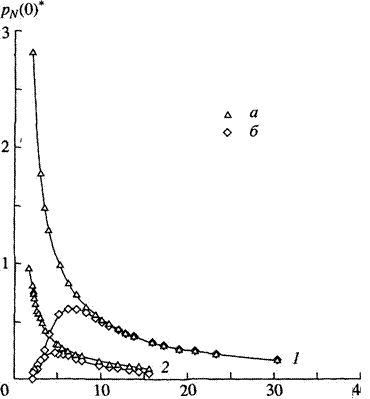
Рис. З. Зависимость давления р: (О) в центре капли от радиуса R * эквимолекулярной разделяющей поверхности: 1 — потенциал Юкавы. Т = 0.40Тс; 2 — потенциал Леннард-Джонса. Т = 0.51 Тс. а — капиллярное приближение; б — нормальная компонента тензора давления в центре капли.
меньших 10d. Немонотонное поведение плотности в центре капли в вависимости от ее размера также обнаруживается в рамках градиентного разложения в методе функционала плотности [13].
Аналогичная по характеру
зависимость плотности в центре капли от радиуса эквимолекулярной разделяющей
поверхности была обнаружена и при моделировании капли методом молекулярной
динамики [14]. Последнее может служить подтверждением применимости метода функционала
плотности даже для малых капель, толщина поверхностного слоя которых порядка
нескольких межатомных расстояний. ![]()
Наличие эффекта самопереКрытия позволяет говорить о существовании в малых гомогенно зародившихся каплях аналога расклинивающего давления, которое обычно наблюдается в тонких жидких пленках. Сказанное может быть проиллюстрировано с помощью зависимостей, изображенных на рис. 3. На этом рисунке представлены нормальная составляющая тензора давления в центре капли, вычисленная по формуле
РИ О ) = Р$( О ) =
(4.4)
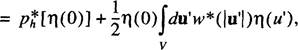
и классическое капиллярное приближение для давления в капле
р Уар + (4.5)
где давление жидкой фазы руар и давление пара р! определены при химическом потенциале капли у, — безразмерное поверхностное натяжение для плоской поверхности раздела между жидкостью и паром, которое связано с размерным поверхностным натяжением формулой о! = пГо46КБТ. (4.6)
Для нахождения 000 использовалось соотношение, вытекающее из термодинамического определения поверхностного натяжения:
![]() (4.7)
(4.7)
где „400 — площадь поверхности раздела фаз, индекс указывает, что все величины определены в пределе плоской границы раздела при равновесии жидкости и пара.
В области малых R * наблюдается сильное расхождение кривых (4.4) и (4.5), при этом р: (О) проявляет немонотонное поведение. Имея в виду определение расклинивающего давления для тонкой пленки, разность давлений, вычисленных по формулам (4.5) и (4.4), можно назвать аналогом расклинивающего давления в малых гомогенных каплях.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.