Термодинамические характеристики малой капли в рамках метода функционала плотности, страница 3

Следуя [2, З], в качестве начального приближения возьмем профиль

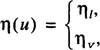U<U,

(3.6)

Наиболее оптимальный выбор характерного начального параметра вычислительной схемы и

можно осуществить, проследив поведение числа частиц в системе в ходе итерационного процесса. При значениях и больше некоторого и*, начиная с определенного момента число частиц в системе неуклонно возрастает, это отвечает устойчивой сходимости к однородной жидкости. При значениях и меньше и*, начиная с некоторого момента, число частиц в системе убывает, что отвечает устойчивой сходимости к однородному пару. Всегда можно выбрать значение и так, чтобы оно лежало как можно ближе к в пределах одного шага разбиения оси и при численной реализации решения задачи.

Помимо параметра и при численном решении возникает еще один параметр L, который определяет верхнюю границу изменения переменной и. При достаточно больших L можно считать, что в области и > L плотность достигает своего объемного значения. Выбор параметра 1., зависит от толщины переходного слоя, которая изменяется с температурой. Значение L, однако, не стоит изменять при переходе от одного значения џ* к другому (при фиксированных значениях температуры Т и числе интервалов разбиения), т.к. это может привести к нефизичным скачкам в поведении профилей плотности и зависящих от них термодинамических величин.

Для того чтобы определить, на какой итерации следует оборвать итерационный процесс, мы наблюдали, следуя [1, 2], за поведением большого термодинамического потенциала системы П* После нескольких первых итераций, в ходе которых происходит сглаживание профиля плотности, потенциал практически перестает изменяться. Это означает, что мы находимся в окрестности критического зародыша. Когда решение уходит из этой окрестности, вновь начинает резко убывать. Для того чтобы выбрать наиболее подходящее приближение, мы следили за ходом следующих величин

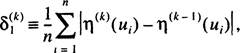            (3.7)

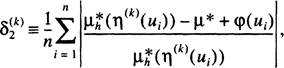        (3.8)

где п — число точек разбиения, — номер точки разбиения, К — номер итерации, (Р(иД — интеграл в левой части уравнения (3.1). Величины 5(l^k) и 62

достигают своего минимуМа почти при одинаковых К. При этих значениях К и происходило завершение итерационного процесса.

Мы провели вычисления профиля тт(и) для двух значений температуры Т/Тс = 0.40 и Т/Тс = 0.80 для

КОЛЛОИДНЫЙ

метр потенциала Юкавы) и при Т/Тс = 0.51 и Т/Тс = 0.80 для потенциала Леннард-Джонса (Тс = = 1.488Е/КБ', Е — параметр потенциала ЛеннардДжонса). Характерные результаты представлены на рис. 1. Видно, что при 77 Тс = 0.80 значения плотности в центре капли и в паре различаются в десятки раз, при этом толщина переходного слоя оказывается порядка 15d. При Т/Тс = 0.40 и П Тс = 0.51 плотности различаются уже в 10³ раз (что характерно, например, для нуклеации в парах в атмосферных условиях), а толщина переходного слоя становится порядка 5d.

4. НЕОДНОРОДНОСТЬ ЦЕНТРАЛЬНОЙ

ОБЛАСТИ МАЛОЙ КАПЛИ

При изучении профилей плотности, полученных в результате решения уравнения (3.1), обраищет на себя внимание тот факт, что плотность в центре капли может не достигать своего значения ту, соответствующего однородной жидкости. Более того, в малых каплях практически нет однородного участка в центральной области. Можно говорить лишь о локальной однородности в центре зародыша в малой окрестности точки и = 0, где всегда выполняется условие

С увеличением размера капли объем однородной области рдстет, а плотность в центре капли приближается к значению, присущему объемной жидкой фазе при том же значении химического потенциала џ*.

Неоднородность центральной области малой капли при гомогенной нуклеации можно рассматривать как результат самоперекрытия поверхностного слоя малых зародышей аналогично перекрытию поверхностных слоев при гетерогенной нуклеации [11]. Для того чтобы проследить, какое влияние оказывает этот эффект на поведение различных термодинамических величин, необходимо ввести переменную, характеризующую размер зародыша.

В качестве такой переменной выберем радиус Rе эквимолекулярной разделяющей поверхности, определяемый условием