3. Свободные колебания одноосного вагона с учетом упругости пути.
3.1. Математическая модель и её решение
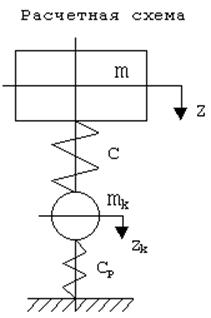
Для выбора расчетной схемы принмем следующие допущения.
Части вагона обладают только свойствами инерции, упругими свойствами не обладают.
Рессорное подвешивание и путь обладают только упругими свойствами, свойствами инерции и трения не обладают.
 |
Уравнение движения:
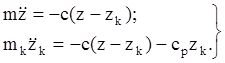 (1)
(1)
Преабразуем систему (1): раскроем скобки,
разделим каждое равнение на коэффициент
при старшей производной, перенесем все
члены в право и введем обозначения:
![]()
В результате получим систему уравнений
в следующем виде:
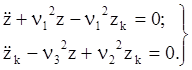 (2)
(2)
Решение системы ищем в виде следующих функций:
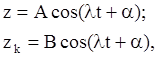 (3)
(3)
где A,B,![]() -неизвестные постоянные
величины.
-неизвестные постоянные
величины.
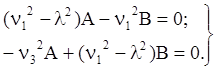 (4)
(4)
В результате получена алгебраическая система двух однородных уравнений, но с тремя неизвестными. Известно, что любая система однородных уравнений имеет не нулевое решение только в случае равенства нулю её определителя. Выпишем определитель и приравняем его к нулю. Такой определитель называется характеристическим.
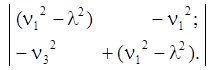 (5)
(5)
Раскрыв определитель получим характеристическое уравнение относительно λ2:
![]()
Найдем корни этого уравнения, обозначив их через λ12 и λ22:
![]()
Упростим подкоренное выражение
![]()
Заметим следующую зависимость между собственными частотами и парциальными частотами:
![]() .
.
Оценим знак разности
![]() ;
;
![]()
Из последнего выражения
следует, что: ![]() < 0;
< 0; ![]() > 0.
> 0.
Аналогично можно получить,
что: ![]() > 0;
> 0; ![]() <
0.
<
0.
Используя полученные результаты построим общее решение поставленной задачи.
Частное решение системы (2):
при λ = λ1
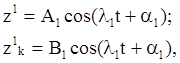
при λ = λ2
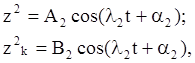
Общее решение построим как сумму частных:
![]()
![]()
Полученное
решение содержит
шесть
неизвестных нам постоянных величин: A1,A2,B1,B2,α1
и α2. Для определения неизвестных величин можно задать только четыре
начальных условия: z=z0, ![]() и zk=zk0,
и zk=zk0, ![]() . То есть только начальных
условий не достаточно.
. То есть только начальных
условий не достаточно.
Вернемся к системе алгебраических уравнений (4) и подставим в неё поочередно конкретные значения λ=λ1 и λ=λ2. В результате дважды получим алгебраическую систему с равным нулю определителем.
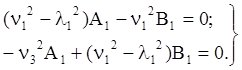
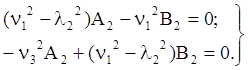
Это говорит о том, что получены не системы из двух уравнений, а дважды по одному уравнению в разных видах. Их них можно определить только отношения неизвестных величин.
Из первых двух уравнений следует:
B1/A1 = ν22-λ12/ν12 =ν32/ν12-λ12 =![]() 1>0.
1>0.
Из вторых: B2/A2 = ν22-λ22/ν12 =ν32/ν12-λ22 =![]() 2<0.
2<0.
Полученные выражения – отношения амплитудных значений координат при колебаниях изучаемой системы с её собственными частотами называются собственными или главными формами колебаний. Они как и собственные частоты не зависят от начальных условий и являются динвмическими свойствами изучаемой системы.
Теперь,
с учетом, что B1=A1·![]() 1 и B2=A2·
1 и B2=A2·![]() 2 общее решение примет вид
содержащий только четыре неизвестных величины:
2 общее решение примет вид
содержащий только четыре неизвестных величины:
![]()
![]()
Четырех нечальных условий достаточно для их однозначного определения.
3.2. Графическое представление собственных форм
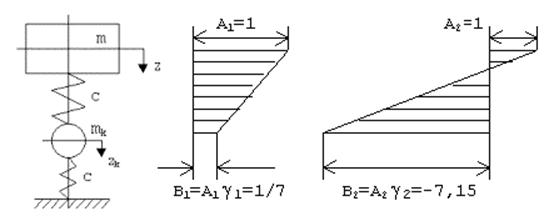
Для грузового вагона в одном
из режимов загрузки ![]() 1=1/7;
1=1/7;![]() 2=-7,15.Графически это можно
изобразить, например, так:
2=-7,15.Графически это можно
изобразить, например, так:
 |
 |
Парциальные системы и парциальные частоты
Первая парциальная система – закреплена координата zk.
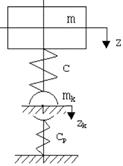
Уравнение движения
![]()
Первая парциальная частота
![]() .
.
Вторая парциальная система– закреплена координата z.
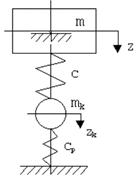 |
Уравнение движения
![]()
![]()
3.3. Заключение
Проведенный анализ позволяет заключить следующее.
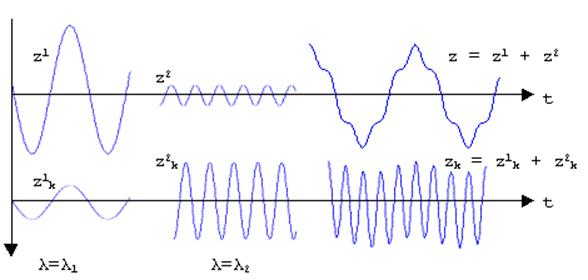
1. Как кузов, так и неподрессоренные части вагона при свободных колебаниях движутся со всеми собственными частотами присущими ему как динамической системе.
2. Основной систавляющей колебаний кузова является движение с низшей собственнной частотой, λ1, колебания с высокой частотой, λ2, проявляются на кузове в виде вибраций с незначительной амплитудой.
3. Основной систавляющей колебаний неподрессоренных частей является движение с высокой собственнной частотой, λ2, колебания с низшей частотой, λ1, проявляются на них с незначительной амплитудой.
4. При первой собственной форме
колебаний (колебания только с частотой λ1) кузов и неподрессоренные части движутся в фазе, то
есть в одном направлении, так как ![]() >0. Колебания
при второй собственной форме (колебания только с частотой λ2) кузов и неподрессоренные
части движутся в противофазе, – то есть в разных направлениях, так как
>0. Колебания
при второй собственной форме (колебания только с частотой λ2) кузов и неподрессоренные
части движутся в противофазе, – то есть в разных направлениях, так как ![]() >0.
>0.
5. Собственные формы колебаний позволяют определить связность колебаний частей системы по обобщенным координатам и проявляются в резонансных режимах.
6. Зная собственные частоты и связность колебаний частей системы по обобщенным координатам можно определить количество и величины критических или резонансных скоростей движения вагона.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.