Движение колесной пары по рельсовому стыку

Движение колесной пары по рельсовому стыку

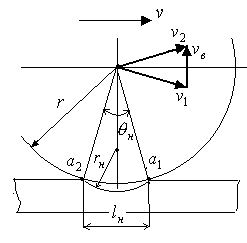
При перекатывании колесной пары через стыковое соединение рельсов (рельсовый стык) происходит скачкообразное перемещение мгновенного центра вращения с отдающего конца рельса на принимающий. Это приводит к  мгновенному изменению направления вектора скорости центра масс колесной пары за счет мгновенного возникновения вертикального вектора скорости. А мгновенное приложение вектора скорости – удар. Таким образом, при перекатывании колесной пары через рельсовый стык происходит ударное взаимодействие колеса и рельса. Схема прохождения колесной пары через рельсовый стык показана на рис. 1.

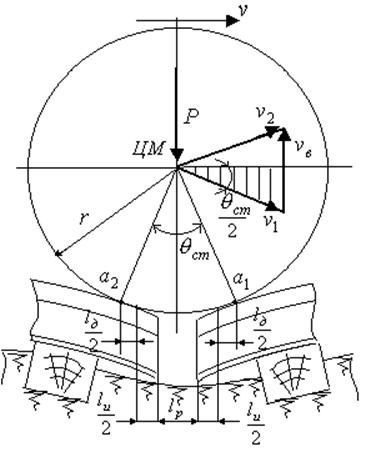Непосредственно из рис. 1. следует, что вектор скорости ЦМ до удара, перпендикулярен радиусу  ЦМ- и обозначен через , а после удара – радиусу  ЦМ- и обозначен через . Изменение произошло за счет возникновения вертикального вектора . Определим величину этого вектора из заштрихованного треугольника

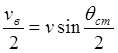, с учетом малости угла можно заменить 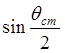 на   и в результате получим                               ,

где  – поступательная скорость движения колесной пары по рельсовому пути;

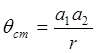– угол, образованный радиусами       

 колеса, ограничивающими дугу, примерно  равную расстоянию между точками касания

      Рис. 1. Колесо на рельсовом стыке                  колесом концов соседних рельсов.

Угол  является суммой трех углов, зависящих от зазора между концами соседних рельсов, дополнительного износа концов рельсов и упругой деформации стыкового соединения под давлением колеса: .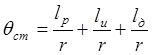

Для определения ударного импульса, возникающего в момент прохождения колесной парой стыкового соединения можно воспользоваться гипотезой А.М. Годыцкого – Цвирко, согласно которой количество движения, приобретаемое колесной паро за время удара, равно импульсу сил, сообщенному ей за это же время, т.е.    ,

где  – масса колесной пары с учетом необрессоренных частей тележки;

        – вертикальная скорость ЦМ до удара;

        – то же после удара.

Принимая , получим  . По определению ударный импульс равен произведению силы удара на время её действия, т.е.  , откуда 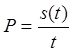. Так как  время удара весьма мало (~), то сила удара оценивается значительными величинами.

Частота воздействия рельсовых стыков определяется следующим образом

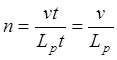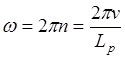 – число воздействий в единицу времени на пути ;  – частота воздействий в Гц;               – частота воздействий рад/с.

Пример: если  ;  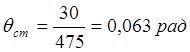;  ; , то

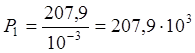 ;  Н, (20,79 тс);

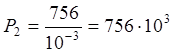;      Н, (75,6 тс)

Прохождение колесной парой короткой неровности с  , аналогично прохождению рельсового стыка и показано на  рис. 2.

              ;   ;   ;   

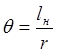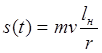
                       Длина рельсовых звеньев                                          

С увеличением длины рельсовых звеньев уменьшается количество стыковых соединений и нарушений равномерности свойств  пути, что способствует увеличению срока службы пути и Рис. 2.  Прохождение колесной        подвижного состава. Поэтому общей тенденцией в мире                                     

 парой короткой неровности        является увеличение длина рельсовых звеньев.

 Нормальная длина рельсовых звеньев ()  в различных странах колеблется в пределах 12 – 60 м.

                                           , м                       Страны 

25  СНГ

11,89                       США          

18 и 24                    Франция

24 и 48                    Чехия

20 и 25                    Япония

30, 34,  60               Германия

В настоящее время в России и за рубежом широко используется бесстыковой (бархатный) путь. Преимущества применения такого пути:

·  сбережение металла за счет стыковых скреплений;

·  снижение динамического взаимодействия ходовых частей и пути;

·  ликвидация дефектов по стыковым скреплениям;

·  снижение сопротивления движению;

·  сокращение расходов на ремонт и содержание пути и подвижного состава.

Опытная укладка длинных сварных рельсовых плетей началась в 30–их годах прошлого века, в СССР  1936 году. В зависимости от способа соединения рельсовых плетей могут быть:

a)  пути с уравнительными рельсами;

b)  пути с уравнительными приборами.