|
Параметр |
Обозначение |
Размерность |
8-осный полувагон тара 0,5 загрузки брутто |
|||
|
Вид загрузки |
1 |
2 |
3 |
4 |
||
|
Масса кузова |
M |
т |
19,3 |
91,45 |
144,3 |
144,3 |
|
Моменты инерции кузова |
Ix Iy Iz |
т·м2 |
50,0 1170,0 1170,0 |
168,7 4800,0 4800,0 |
200,0 5300,0 5300,0 |
200,0 5300,0 5300,0 |
|
Коэфф. жесткости подвешивания |
Cz Cy |
кН/м |
8000,0 8000,0 |
8000,0 9500,0 |
8000,0 11000,0 |
8000,0 11000,0 |
|
Продольные полубазы |
L1 L2 |
м |
8,5 8,5 |
8,3 8,7 |
8,3 8,7 |
8,3 8,7 |
|
Поперечные полубазы |
B1 B2 |
м |
1,02 1,02 |
0,92 1,12 |
1,02 1,02 |
0,92 1,12 |
|
Положение центра масс |
H |
м |
1,2 |
1,5 |
1,83 |
1,83 |
|
Длина неровности |
LN |
м |
12,5 |
|||
|
3 |
Алексеева Н.В. |
4 |
9 |
8-осный полувагон |
1, 2 |
Задание на курсовую работу по дисциплине "Динамика вагонов" для студентов заочного обучения
Вариант 4
(Исходные данные даются преподавателем. Таблица_lr3.doc)
Раздел 1 Изучение динамических свойств вагона с одноступенчатым подвешиванием
Цель работы. Определить собственные частоты, собственные формы колебаний (СФК), связность колебаний по обобщенным координатам и критические (резонансные) скорости движения вагона при различных условиях симметрии загрузки кузова.
Основы исследования. Теоретические основы свободных колебаний динамических систем (см. файл СвобКолУпрПуть.doc).
Средства исследования. Цифровое моделирование на компьютере.
Понятия. Определения. Критерии
На процессы колебаний динамической системы под действием возмущения определяющее влияние оказывают её динамические свойства: величины собственных частот, собственные (главные) формы колебаний и степень демпфирования собственных форм.
Существенной характеристикой качества упругого подвеса является степень связности колебаний несомого тела по обобщенным координатам. Идеальным является подвес, при котором колебания несомого тела по каждой из обобщенных координат являются независимыми. В этом случае возмущение, действующее по любой из координат, вызывает колебания только по этой координате. Движений, определяемых другими координатами, возмущаться не будет. Если же на колебания по группе обобщенных координат наложено свойство связности, то возмущение, действующее по любой из координат, вызывает колебания по всем координатам составляющим группу.
При движении динамической системы (вагона или любого другого транспортного средства) значительная связность проявится в том, что резонансы по собственным частотам, соответствующим формам с большим числом связанных координат, будут возникать от возмущающих воздействий, направленных по любой из этих координат, что приведет к расширению интервалов резонансных скоростей движения, а также к появлению нескольких интервалов по одной собственной частоте.
Степень связности колебаний определяется условиями симметрии как развески несомого тела (кузова), так и упругодемпфирующего подвеса и может быть выявлена по связанности уравнений движения математических моделей и по собственным формам колебаний (СФК).
Критерием связности колебаний по обобщенным координатам можно принять разные по величинам смещения контрольных точек (КТ) в СФК, при угловом смещении кузова относительно какой либо из осей, и наличие в одной СФК вертикальных и горизонтальных смещений КТ.
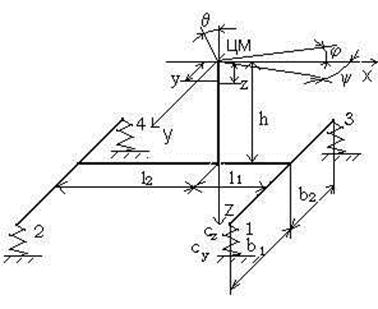
Расчетная схема. Уравнения движения.
Представим
вагон динамической системой с 5-ю степенями свободы, положение которой в любой
момент времени определяется пятью обобщенными координатами. Две из них
линейные - z и y (подпрыгивание и
боковой относ) и три угловые - ![]() (боковая качка,
галопирование и виляние). Начало координат помещено в центр масс кузова (ЦМ), и
расположено над верхней плоскостью опор рессорных комплектов на высоте h. Степень
несимметрии загрузки кузова определяется различием величин продольных (l1,l2) и поперечных
(b1,b2) полубаз. Путь
принят абсолютно жестким, неподрессоренные части на схеме не показаны.
(боковая качка,
галопирование и виляние). Начало координат помещено в центр масс кузова (ЦМ), и
расположено над верхней плоскостью опор рессорных комплектов на высоте h. Степень
несимметрии загрузки кузова определяется различием величин продольных (l1,l2) и поперечных
(b1,b2) полубаз. Путь
принят абсолютно жестким, неподрессоренные части на схеме не показаны.
Расчетная схема
Реакции рессорных комплектов:
|
|
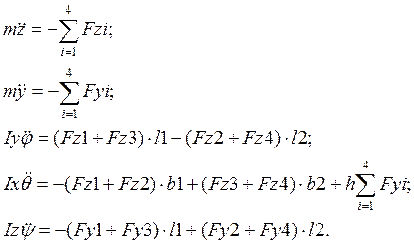 |
Выражения, определяющие деформации рессорных комплектов при смещениях кузова по выбранным обобщенным координатам:
а) вдоль оси zб) вдоль оси y
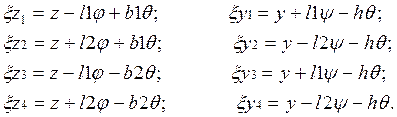
Содержание работы :
1. Познакомиться с разделом "Понятия. Определения. Критерии".
2. Изучить раздел "Расчетная схема. Уравнения движения".
3. Выбрать основные возмущающие факторы.
4. Составить уравнения движения для четырех
случаев загрузки кузова по условиям симметрии: а) l1 ![]() l2, b1
l2, b1 ![]() b2; б) l1
b2; б) l1 ![]() l2, b1 = b2 ;
l2, b1 = b2 ;
в ) l1 = l2, b1 ![]() b2 ; г) l1 = l2, b1 = b. Использовать
выражения для
b2 ; г) l1 = l2, b1 = b. Использовать
выражения для
реакций и деформаций рессорных комплектов.
5. Оценить связность колебаний кузова по уравнениям движения.
6. Работая на компьютере, изучить влияние различных условий несимметрии загрузки кузова на собственные частоты, собственные формы колебаний , связность колебаний по обобщенным координатам, используя раздел "Информация, ориентирующая при работе на компьютере".
7. Провести расчет критических (резонансных) скоростей движения,
приняв в качестве вертикальных возмущений синусоидальную
рельсовую неровность длиной 12,5 м, а в качестве горизонтальных -
виляние колесной пары.
8. Формулировать выводы с их графической иллюстрацией.
9. Оформить отчет.
1. Имя первого рабочего файла на диске D - sch3dml.bat.
2. Имя файла исходных данных ( см.на диске D) - sch2.d
3. Имя файлов результатов расчета (см.на диске D) - sch2mlr.m,
sch2mlra.m, sch2mlrb.m, sch2.r.
4. Имя файла входа в Matlab - ms bat.
5. Имя первого рабочего файла в Matlabe - zform1.m (будет обработан
один вариант расчета).
6. Имя второго рабочего файла в Matlabe - zform1a.m (будет обработано
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.