










План лабораторной работы № 4
Измерение параметров объекта с помощью лабораторной ИИС
Цель работы:
¾ научиться определять параметры случайных событий с целью изучения их свойств.
Задачи работы:
¾ получить знание и умения регистрации параметров физических величин, как независимых, так и зависимых от времени;
¾ научиться методу определения величины параметров внутри дискретных интервалов измерения параметров объектов;
¾ преобрести навыки вычисления значений функционалов средствами ИИС;
¾ Знакомство с основными моделями, применяемыми для вычисления функционалов и оценки неопределенности измерений.
1. Некоторые способы измерений с помощью лабораторной ИИС
1.1. Регистрация исследуемых физических величин независящих от времени
Порядок измерения и обработки результатов измерений ИИС зависит от многих факторов [1], [2], [4], [6]. Простейшая задача регистрации измеряемых физических величин может не иметь алгоритма обработки результатов измерений, так как опрос каналов осуществляет своими командами ЭВМ. Единственное, что может понадобиться, это введение поправок и сглаживание информационного объема данных перед моментом отправки результатов измерений потребителю. Необходимость в дискретизации по времени тоже в данном случае исключается. Такое измерение предусматривает лишь сохранение в памяти всех отображаемых результатов.
1.2. Регистрация исследуемых физических величин зависящих от времени
В случае зависимости измеряемых параметров от времени опрос измерительных каналов так же осуществляет ЭВМ, но при этом для измерения задается фиксированные интервал времени. Полученные результаты измерений одновременно, последовательно или Группами, которые получены с помощью программных средств, отображаются на многоканальном осциллографе или мониторе, который работает режиме многоканального осциллографа.
В данном случае, в силу необходимости, тоже вводятся поправки и сглаживается первичная измерительная информация, а так же массив данных отправляется на долгосрочное хранение.
В месте с тем появляются две новые взаимосвязанные задачи:
• анализ влияния дискретизации по времени на погрешность регистрации функций;
• выбор более удобных, компактных форм представления полученных результатов измерений.
1.3. Определение величины измеряемых параметров внутри интервала дискретного времени опроса измерительных каналов ИИС
Для получения значений измеряемых параметров внутри дискретного времени опроса измерительных каналов применяют метод интерполяции – описывают поведение параметра внутри дискретного времени какой-либо функцией. Естественно, для выбора функции следует априори знать, хотя бы примерно, вид функциональной зависимости параметров от времени.
Если измеряемый параметр не зависит от времени, но измерение выполняется по времени дискретно, то интерполяция дает потребителю существенно увеличенную измерительную информацию, что делает такую операцию метрологически некорректной.
Если ИИС обрабатывает результаты косвенных, совместных или вероятностных характеристик, то увеличения объема информации, выдаваемого потребителю не происходит и часто даже уменьшается.
Интерполяция может проводиться либо во временной области, на основе разложения функции, например, в ряд Тейлора, либо в частотной области на основе теоремы Котельникова (см. приложение 6 [1]).
1.3.1. Интерполяция рядом Тейлора
Пусть измерили параметр ![]() с
периодом дискретного опроса равного
с
периодом дискретного опроса равного ![]() .
Предполагая, что в интервале
.
Предполагая, что в интервале ![]() параметр
параметр
![]() является
непрерывной функцией времени, применяем для этого параметра разложение в
усеченный (конечный) ряд Тейлора для нужной нам временной точки
является
непрерывной функцией времени, применяем для этого параметра разложение в
усеченный (конечный) ряд Тейлора для нужной нам временной точки ![]() :
:
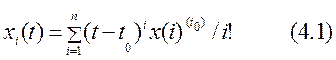
Чтобы получить ![]() производных
нужно выполнить
производных
нужно выполнить ![]() измерений
на временном интервале
измерений
на временном интервале ![]() ,
где
,
где ![]() время двух
соседних отсчетов.
время двух
соседних отсчетов.
На первом этапе, для понимания исследуемого процесса, используют линейную интерполяцию, ограничиваясь в ряде Тейлора первым членом разложения (рисунок 4.2, ломаная линия 1). В дальнейшем используют, по мере уточнения результата, интерполяцию используя члены ряда более высокого порядка (рисунок 4.2, кривая 2).
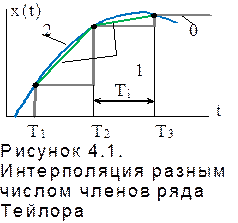
На рисунке 4.1 ступенчатая фигура, обозначенная символом «0», и
выполнена при ![]() .
При
.
При ![]() используется
кусочно-линейная интерполяция (кривая 1), и при
используется
кусочно-линейная интерполяция (кривая 1), и при ![]() уже можно
использовать кусочно-параболическую интерполяцию (кривая 2). Увеличивая число
точек эксперимента, можно использовать для интерполяции кривые более высокого
порядка.
уже можно
использовать кусочно-параболическую интерполяцию (кривая 2). Увеличивая число
точек эксперимента, можно использовать для интерполяции кривые более высокого
порядка.
Чтобы оценить погрешность рассмотренного метода интерполяции, вычисляют последний отбрасываемый член ряда и сравнивают допустимую погрешность с величиной отброшенного члена ряда. Результат считают удовлетворительным, если выполняется неравенство (4.2)
![]()
На рисунке 4.1 хорошо видно, что парабола проводится через три точки, значит среднюю точку можно в эксперименте не пприводить. С ростом числа членов ряда число таких точек еще увеличивается, что уменьшает массив измеряемой информации для потребителя. При желании эти результыты можно получить с помощью программного продукта ИИС.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.