Измерение параметров объекта с помощью лабораторной ИИС. Регистрация исследуемых физических величин независящих от времени, страница 4

3.1.2.   Экспериментально определить погрешность реального ПМО.

3.1.3.   Экспериментально определить суммарную погрешность объекта измерений и измерительного канала.

3.1.4.   По техническим характеристикам ПИП и результатам измерений вычислить погрешность ИК и сравнить ее с экспериментальными результатами.

3.1.5.   Получить у преподавателя по варианту объект измерения.

3.1.6.  Получить измерения параметра объекта не менее 50 раз с интервалом времени соответствующем теореме Котельникова.

3.1.7.  Поместить полученные результат в программный продукт обработки результатов измерений и получить

·  ступенчатый график функции;

·  график кусочно-линейной интерполяции;

·  график кусочно-квадратичной линейной интерполяции.

3.1.8.  Выборочно экспериментально проверить результаты интерполяции для 10 точек и определить неопределенность для каждого вида интерполяции в этих точках.

3.1.9.  Сделать выводы о том, какой вид интерполяции позволяет получить меньшую неопределённость интерполяции.

3.2   Измерение функциональной зависимости параметра объекта от времени

3.2.1.   Получить у преподавателя по варианту объект измерения.

3.2.2.  Получить измерения параметра объекта не менее 50 раз с интервалом времени соответствующем теореме Котельникова.

3.2.3.  Получить у преподавателя вид ортогональных функций для восстановления дискретной функции в непрерывную.

3.2.4.   Выборочно по эксперименту и результатам восстановления функции определить погрешность восстановления функции.

3.2.5.   Исследовать несколько точек на одном интервале отстета результатов измерения и поместить их в таблицу с фактическими значениями функции.

3.2.6.   Сделать выводы о том, где на интервале опроса расхождение фактической и восстановленной функции наибольшее.

3.3.   Измерение функционалов

3.3.1.   Выбрать для своего варианта из таблицы 1 результаты измерений функционально зависимых параметров.

3.3.2.   Используя кусочно-линейную интерполяцию, качественно определить вид полученной функциональной зависимости.

3.3.3.   Используя программный продукт, например программу “Excel”, более точно провести интерполяцию, дополнительно качественно убедившись в правильности сделанного вывода о типе функции.

3.3.4.  Взять промежуточные значения аргумента для данной функции и для этих точек выполнить интерполяцию.

3.3.5.   Повторить п. 3.3.3 настоящего задания.

3.3.6.   Сравнить результаты полученные в п. 3.3.3 и п. 3.3.6.  Графически оценить расхождение результатов измерений образов функции.

3.3.7. Используя пассив данные таблицы 4.1 для своего варианта и массивы данных промежуточных значений вычисленных Вами, повторить пункт п. 3.3.3.

3.3.8.    По результату п. 3.3.7 сделать вывод о правильности принятого Вами решения. Указать неопределенность результатов, полученных в п. 3.3.7.

3.3.9.   Найти функционалы от полученной функции. Пределы интегрирования выбрать такими: от 0,1 до 0,5; от 0,1 до 1,0; от 0,1 до 1,5; от 0,1 до 2,0; от 0,1 до 2,5; от 0,1 до 3,0.

3.3.10.   Произвольно выбрав интервалы по оси абсцисс, построить график зависимости функционала от величины интервала интегрирования.

3.3.11.   Сделать качественно вывод о линейности или нелинейности полученной зависимости.

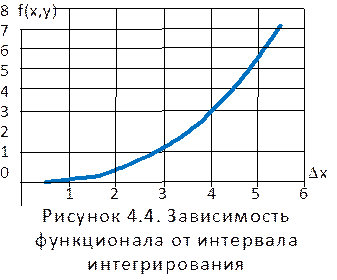
3.3.12. Пусть мы узнали, что кусочно-линейная аппроксимация позволила нам сделать вывод о том, что функция похожа на зависисмость типа . После интегрирования в интервалах, указанных в п. 3.3.9 получаем значение функционалов: 0,012; 0,3025; 0,96; 2,205; 4,225; 7,2075. На рисунке 4.4 эта зависимость представлена графически. 

Делаем вывод, что эта зависимость нелинейная. Предыдущие пункты задания легко  с 3.3.4 по 3.3.9 выполнить легко, спользуя возможности, например, программы Excel.

4 Содержание отчета

4.1 Стандартный титульный лист.