1.3.2. Определение интервала дискретности по теореме Котельникова
При определении периода дискретизации в частотной области базируются на
теореме Котельникова, доказательство и комментарии к которой приведены в
приложении 6 [1]. В соответствии с этой теоремой сигнал, спектр которого равен
нулю вне полосы частот ![]() ,
может быть полностью восстановлен по своим отсчетам, за период времени, при
выполнении неравенства (4.3)
,
может быть полностью восстановлен по своим отсчетам, за период времени, при
выполнении неравенства (4.3)
![]()
Для восстановления сигнала по его отсчетам требуется идеальный фильтр нижних частот, который при реализации на ЭВМ приведет к дискретной свертке, то есть интерполируемая функция в любой момент времени будет выражаться через сумму всех отсчетов, умноженных на соответствующие коэффициенты. Структура преобразований входных данных при интерполяции в обоих случаях одинакова.
Второе сходство рассмотренных двух методов интерполяции, это неограниченная дифференцируемость исследуемой функциональной зависимости параметра от времени.
Восстановить функцию математически и практически невозможно абсолютно точно. Во первых, при интерполяции функция не точно определяется рядом Тейлора из-за ограниченности членов его ряда. Во вторых, в частотной области выполнить идеальный фильтр, с П- образной АЧХ, практически невозможно.
1.3.3. Один из методов получение непрерывной функции по дискретно полученным ее значениям при измерении в ИИС
Любая интерполяция приносит не только качественную, но и количественную
информацию. Пожалуй это обстоятельство привело к тому, что для интерполяции
используют многие математические выражения, в частности ортогональные функции ![]() . Ортогональные
функции суммируют, предварительно умножая их на весовую функцию
. Ортогональные
функции суммируют, предварительно умножая их на весовую функцию ![]() , которая
определяет уровень влияния применяемых ортогональных функций на степень
приближения получаемого образа
, которая
определяет уровень влияния применяемых ортогональных функций на степень
приближения получаемого образа ![]() к
реальному образу исследуемого объекта на ограниченном временном интервале
к
реальному образу исследуемого объекта на ограниченном временном интервале ![]() .
Единственное требование для такой интерполяции: исследуемая функциональная
зависимость соответствует непрерывной и дифференцируемой функции на
рассматриваемом интеравале
.
Единственное требование для такой интерполяции: исследуемая функциональная
зависимость соответствует непрерывной и дифференцируемой функции на
рассматриваемом интеравале ![]() .
Итак запишем образ изучаемой функции
.
Итак запишем образ изучаемой функции
![]()
Коэффициенты ![]() для этого
уравнения следует определять по формуле
для этого
уравнения следует определять по формуле
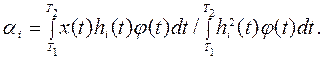
Таким образом, при регистрации функций ИИС выдает совокупность дискретных значений, которые интерполяцией можно описать как непрерывную функцию времени. К сожалению оценить точность образа интерполированной и реальной функции математическим методом невозможно.
Этот метод полностью приемлем для выявления функциональной зависимости параметров между собой. Так функции двух переменных дают на экране плоскую геометрическую фигуру. Снабдив ИИС сканерами, можно расшифровать эти графические образы.
2. Вычисление функционалов средствами ИИС
2.1 Исходные положения для вычисления функционалов
Для оценки погрешностей измерения функционалов и параметров применимы те же соотношения. Однако при этом возникают два практически важных момента.
Момент 1. Если при измерении функции
![]()
известны СКО двух
выборок ![]() и
коэффициент корреляции измереных величин этих выборок
и
коэффициент корреляции измереных величин этих выборок ![]() , то число
аргументов в функциях для вычисления погрешности измерения
, то число
аргументов в функциях для вычисления погрешности измерения
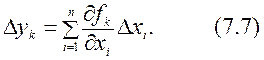
и общей дисперсии
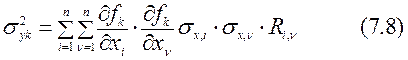
Требуется число
слагаемых в формулах (7.7) и (7.8) равное ![]() , что на
порядки больше, чем при неавтоматизированных совместных измерениях.
, что на
порядки больше, чем при неавтоматизированных совместных измерениях.
Момент 2. Явные аналитические выражения для функций ![]() могут
отсутствовать, алгоритм их вычисления сводится к определению экстремума функции
(7.6) и задается условием обеспечения минимума критерия отличия
могут
отсутствовать, алгоритм их вычисления сводится к определению экстремума функции
(7.6) и задается условием обеспечения минимума критерия отличия ![]() . Дифференцирование
таких функций очень сложно и возможно только численными методами. Оценку
неопределенности измерений без ЭВМ получить быстро по времени невозможно.
Модель в программе ЭВМ должна содержать четыре основных компонента, которые
приведены на рисунке 4.2.
. Дифференцирование
таких функций очень сложно и возможно только численными методами. Оценку
неопределенности измерений без ЭВМ получить быстро по времени невозможно.
Модель в программе ЭВМ должна содержать четыре основных компонента, которые
приведены на рисунке 4.2.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.