Координата центра тяжести элемента 2
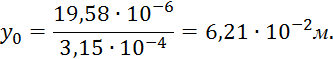
Момент инерции элемента 2
![]()
Геометрические
характеристики всего сечения простенка 1-2 будут иметь следующие значения (при
имеем в виду, что сечение имеет ось симметрии z , поэтому положение центров
тяжести отдельных элементов устанавливается по чертежу, ![]()
![]()
![]() ).
).
Момент инерции сечения простенка 1-2
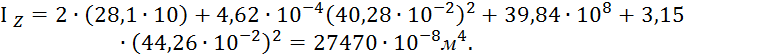
Площадь сечения простенка
F=2![]() =15,6
=15,6![]()
Площадь листа обшивки простенка
![]()
Момент сопротивления простенка
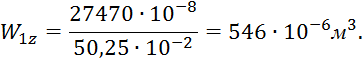
Геометрические
характеристики остальных простенков будут иметь следующие значения: 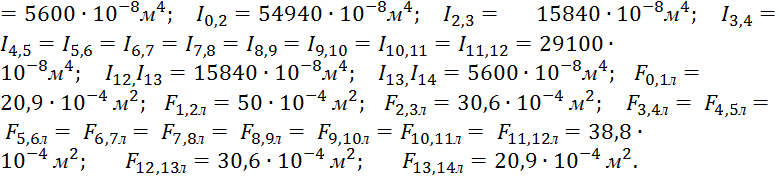
Рисунок 4.6 - Сечение верхнего пояса кузова (а) и иго элементов (б)
Рисунок 4.7-Сечение нижнего пояса кузова (а) и его элементов (б)
Геометрические характеристики поясов
нижнего ![]() =186375
=186375![]()
![]() =151150
=151150![]()
нижнего приведенного
![]() =336525
=336525![]()
Площади поперечного сечения
нижнего
пояса ![]()
верхнего
пояса ![]()
нижнего
приведенного пояса ![]()
Моменты
сопротивления ![]() для
элементов пояса имеют следующие значения:
для
элементов пояса имеют следующие значения:
конька
крыши ![]()
верхней
обвязки ![]()
нижнего
гофра верхнего пояса![]()
верхнего
гофра нижнего пояса ![]() нижней
обвязки
нижней
обвязки ![]()
гофра пола ![]() (см.рис.4.6,
4.7).
(см.рис.4.6,
4.7).
Высота
оконного проема C=0,875м. Модуль упругости
материала металлоконструкции кузова Е=2,1![]() МПа, а модуль сдвига G= 8
МПа, а модуль сдвига G= 8 ![]() МПа.
МПа.
4.3.2 Составление системы канонических уравнений
Внутренние усилия Х в стержнях основной системы (рисунок 4.3) определяется из канонических уравнений метода сил
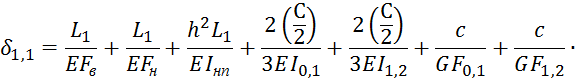
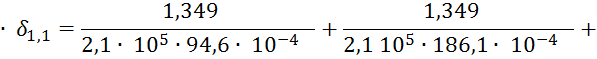
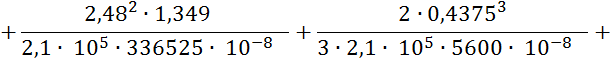
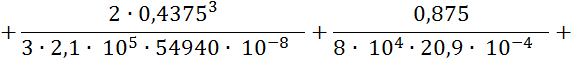
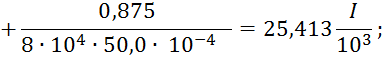
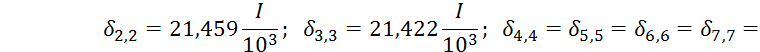
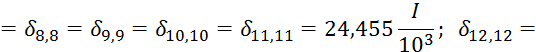
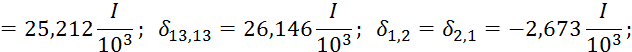
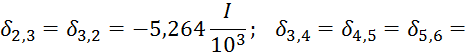
![]()
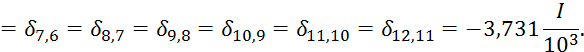
Величины
грузовых членов уравнения определяем следующим образом (рассмотрим участок
длиной ![]() )
)
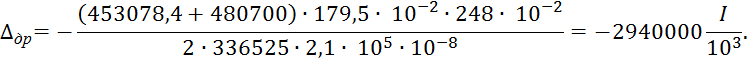
Остальные грузовые члены имеют следующие значения
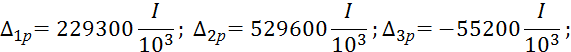
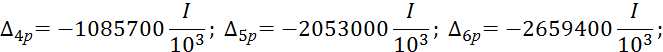
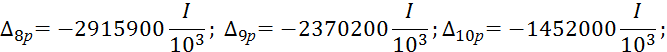
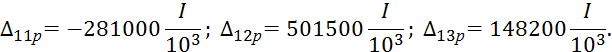
Система
канонических уравнений после сокращения ![]() принимает
вид:
принимает
вид:
25,413![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
При решении системы канонических уравнений получаем значения «лишних неизвестных», указанных на основной системе
![]()
![]()
![]()
![]()
Знак «-» требует поменять направление действия данных сил.
4.3.3 Определение ординат суммарных эпюр
При построении суммарной эпюры изгибающих моментов по поясам имеем в виду следующее. В сечениях 3-3 и 14-14 (в зонах опоры кузова на тележку) сосредоточенное действие реакции шкворневых балок передается только на нижний пояс кузова. Поэтому в этих сечениях необходимо ординаты Мнш увеличить на величину б, а ординаты Мвш - соответственно уменьшить. Определим следующим образом. По формуле (4.7) и (4.8)
вычисляем ординаты Мв2 , Мвш и М1в2 , откладываем их в сечениях 2-2, 3-3 и 4-4 (рисунок 4.7), фиксируем вершины отложенных ординат (точки а, б, с), соединяем точки «а» и «о» находим точку «д» и в масштабе определяем ординату отрезка «дб» который и является поправочной величиной б. Кроме того, при построении суммарной эпюры изгибающих моментов по поясам (рисунок 4.7а) необходимо производить «спрямление» ординат в зонах их примыкания к простенкам, чтобы устранить скачки ординат, обусловленные влиянием на одно и то же сечение внутренних усилий от двух смежных оконных проемов. За порядком спрямления эпюры проследим строя ее по двум оконным проемам 4 и 5 верхнего пояса (рисунок 4.7а). Вычислив по формуле (4.7) ординату эпюры МВ4 для сечения 5-5 с учетом внутренней силы Х4 откладываем ординату (положительную - вверх, отрицательную - вниз). Затем аналогично вычисляем и откладываем ординату М1в4 для сечения 6-6 с учетом той же силы Х4. Вершины отложенных ординат в сечениях 5-5 и 6-6 соединяем между собой, а затем проводим линии от кромок четвертого окна до пересечения линии эпюры и получаем точки А и. В. Аналогично производим построение эпюры по пятому оконному проему. Вычисляем и откладываем ординаты Мв5 и М1в5 , проводим линии от кромок пятого окна и получаем точки С и Д. Соединив точки В и С в зоне простенка 4-5, получаем спрямленную эпюру в сечении 6-6. Точно так же производим спрямление эпюры на всем протяжении длины обоих поясов. Суммарные эпюры Нв, Нд, Мi, I +1 (рисунок 4.7б) отроим обычным порядком.
![]() ,
(4.7)
,
(4.7)
![]() , (4.8)
, (4.8)
Величина изгибающего момента по верхнему поясу
![]() ,
,
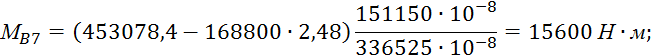
![]() ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.