Расчет кузова на прочность. Техническая характеристика кузова и исходные данные для расчета вагона на прочность, страница 3

Расстояние между центрами тяжести верхнего и нижнего поясов принимаем по всей длине кузова постоянным h = 2,48 м (исключением являются дверные проемы). Расчетная схема тринадцать раз статически неопределима. Основная система указана на рис. 4.4б.

Ординаты эпюры изгибающих моментов М _Кi, действующих по нижнему поясу кузова, определяем как для статически определимой балки на двух опорах с двумя консолями и составляют

        М _К1  =  - 32290 Н∙ м;         М _К2 =  - 108520 Н∙ м;      М' _К2 =  - 170490 Н∙м;

М _К3  = - 83670 Н ∙ м;        М _К4 = 81770 Н∙ м;           М _К5 = 262760 Н∙ м;

М _К6  = 389290 Н ∙ м;                                                                                        М _К7  = - Р1 ( l₀ +  l₁ +  l₂ + l₃ + l₄+ l₅ + l₆) – Р2 (  l₁ +  l₂ + l₃ + + l₄+ l₅ + l₆ – 0,4195) - ∙ 3,3 ∙+0,6185+ l₃  + l₄+ l₅ + l₆) – ∙ 1,9 + 0,0325 +      + l₄+ l₅ + l₆) – ∙ 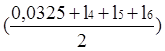+ R1∙ (0,6185+ l₃  + l₄+ l₅ + l₆) =461358,4 Н∙ м;

М_К8 = 478960 Н∙ м;        М_К9 =  435500 Н∙ м;         М_К10 = 333670 Н∙ м;

М _К11 = 131340 Н∙ м;        М _К12 = - 51610 Н∙ м;          М _К13 = - 83760 Н ∙ м;

М' _К12 = -153790 Н∙ м;       М _К14 = - 25750 Н∙ м.

Ординаты расчетной эпюры изгибающих моментов Мр устанавливаем по формуле Мрi = Мкi - М_Хр∙i, где М_Хр∙i - величина ординаты изгибающего момента, действующего в рассматриваемом сечении хребтовой балки.

При этом ординаты расчетной эпюры изгибающих моментов получают следующие значения

Мр₁= - 20890 Н∙ м;         Мр₂ = - 83720 Н∙ м;      М'р₂= - 137572 Н∙ м;

Мр₃ = - 60470 Н∙ м;        Мр₄ = 84100 Н∙ м;        Мр₅ = 260620 Н∙ м;

Мр₆= 391300 Н∙ м;           Мр₇= 461358,4 - 8280 = 453078,4 Н∙ м;

Мр₈ = 480700 Н∙ м;         Мр₉ = 429790 Н∙ м;        М р₁₀ = 322760 Н∙ м.

Мр₁₁ = 121846,5 Н∙ м;    Мр₁₂ = -32560 Н∙ м;     М' р₁₂ = -118620Н∙ м;

Мр₁₃ = -5926 Н∙ м;           Мр₁₄ = -13500 Н∙ м.

При определении грузовых членов канонических уравнений используются данные  значения Мрi.

4.3.1  Определения геометрических характеристик    сложных сечений элементов конструкции кузова

Определяем геометрические характеристики поперечного сечения простенка между первым и вторым оконными проемами (рисунок 4.5а,б). Каждая сторона сечения простенка состоит из двух элементов I и 2. Элемент (рисунок 4.5б) делится на 3 простейших:  первый - нижний лист с размерами 37x3 мм, второйвертикальный лист с размерами 55x3 мм и третий - верхний лист с размером 62x3 мм. В системе произвольных координат y¹ - z¹определяем положение центра тяжести каждого элемента, а затем положение центра тяжести всей фигуры, указанной на рисунке.                                                               Определение собственных моментов инерции частей и всего элемента в целом дано в таблице 1.

Таблица1 - Геометрические характеристики z, входящего в межоконный простенок

Элемент	Fi  10-4  ,м2	yi  10-2  ,м2	Fi yi  10-6 ,м3	Fi y2i  10-8 ,м4	I0i  10-8  ,м4
1 2 3	1,11 1,65 1,86	1,85 3,85 7,10	2,05 6,35 13,2	3,8 24,4 93,6	1,26 - 5,95
	4,62	-	21,6	121,8	7,21

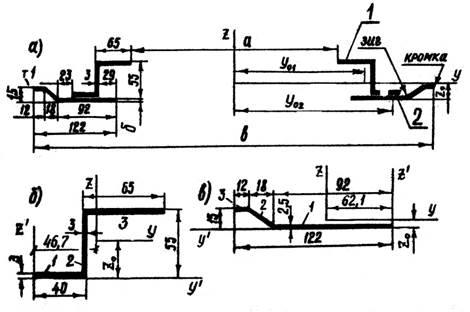
Рисунок 4.5 - Сечение простенка (а) и его элементов (б)

                                                                                                                                                         Координата центра тяжести элемента I определяется по формуле

Момент, инерции элемента I определяется по формуле

Геометрические характеристики элемента 2 (рисунок 4.5а,в) вычисляются аналогичным образом (таблица 2).

Таблица2 -Геометрические характеристики сечения листа водящего в    простенок

Элемент	Fi  10-4  ,м2	yi  10-2  ,м2	Fi yi  10-6 ,м3	Fi y2i  10-8 ,м4	I0i  10-8  ,м4
1 2 3	2,30 0,55 0,30	4,6 10,1 11,6	10,60 5,50 3,48	48,7 56,0 40,3	16,15 0,15 0,04
	3,15	-	19,58	145,0	16,34