Тяговый расчёт. Определение основных удельных сил движения грузовых вагонов на звеньевом пути. Построение диаграммы удельных равнодействующих сил. Решение тормозной задачи, страница 3

4.4. Определение скорости движения, времени хода

поезда графическим методом.

Графическое интегрирование уравнения движения поезда производится по спрямлённому продольному профилю и базируется на следующих предположениях:

1.  Поезд представляется в виде материальной точки, расположенной в середине поезда, причём вся масса сосредоточена в этой точке;

2.  Силы, действующие на поезд в некотором диапазоне изменения скоростей, принимаются с равными значениями.

Суть в спрямлении продольного профиля для производства тяговых расчётов заключается в объединении смежных элементов продольного профиля, которые имеют близкие по значению уклоны одного знака, и замене кривых в плане фиктивными эквивалентными подъёмами в пределах спрямлённых элементов.

Уклон объединённого элемента продольного профиля, определяется по формуле:

,

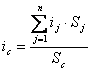где      i_j , S_j – соответственно уклон, %, и длина, м, j-го элемента профиля входящего в объединённый элемент;

S_с – длина объединённого элемента, м.

Проверка возможности спрямления для каждого действительного элемента продольного профиля производится по формуле:

, м,

где      - абсолютная разность между уклоном объединённого и j-го элементов.

Дополнительное сопротивление от кривых в плане, %, определяется по формуле:

 или ,

где       S_кр(j),  R_j ,– длина, радиус, м, и угол,град, j-й кривой в пределах объединённого элемента, м;

            j = 1, 2, ….., n – количество кривых в пределах объединённого элемента.

Результаты по спрямлению схематического продольного профиля и выполнению проверок, сведём в таблицу 22.