Амплитудная спектральная диаграмма чётной периодической последовательности прямоугольных импульсов

Содержание

1 Задача 1…………………………………………………………………....…...4

2 Задача 2……………………………………………………………………......12

3 Задача 3………………………………………………………………….…....21

4 Задача 4……………………………………………………………………......27

5 Задача 5……………………………………………………………………......27

Список использованных источников ………………………………………….33

Приложение А Задача 1…………………………………………….................34

Приложение Б Задача 2 …………………………………………………………37

Приложение В Задача 3 ………………………………………………………..39

Приложение Г Задача 5………………………………………………………..40

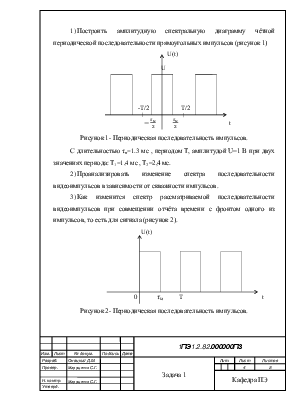
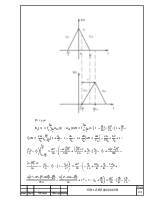
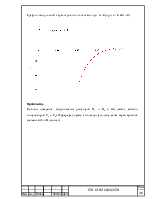
1)  Построить амплитудную спектральную диаграмму чётной периодической последовательности прямоугольных импульсов (рисунок 1)

          U(t)

                                                                 U

                                                  -T/2                   T/2

                             t

Рисунок 1- Периодическая последовательность импульсов.

С длительностью τ_и=1.3 мс , периодом Т, амплитудой U=1 B при двух значениях периода: Т₁=1,4 мс , Т₂=2,4 мс.

2)  Проанализировать изменение спектра последовательности видеоимпульсов в зависимости от скважности импульсов.

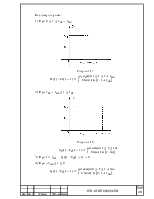
3)  Как изменится спектр рассматриваемой последовательности видеоимпульсов при совмещении отчёта времени с фронтом одного из импульсов, то есть для сигнала (рисунок 2).

                                                    U(t)

                                          0                     T                                                t

Рисунок 2- Периодическая последовательность импульсов.

Решение:

Для решения данной задачи необходимо внимательно прочитать параграф 2.1 учебного пособия [5] и обратить внимание на формулы (1.1) и (1.2) ряда Фурье и его коэффициентов для периодического сигнала. Для решения данного сигнала задачи необходимо провести аналитический вывод формул для коэффициентов ряда и записать окончательную формулу ряда Фурье.

1)  Введём основную частоту по формуле  последовательности, образующий периодический сигнал. Вычисляя коэффициенты разложения , запишем ряд Фурье, для периодического сигнала:

                 (1.1)

Коэффициенты которого вычисляется по формулам:

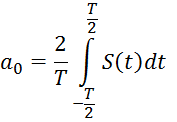
                             (1.2)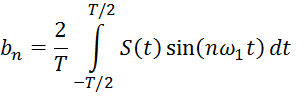

Из формул для коэффициента ряда Фурье следует, что чётный сигнал имеет только косинусоидальные, а нечётный - только синусоидальные слагаемые.

Так как наш сигнал U(t) представляет из себя симметричную (чётную) периодическую функцию с периодом Т (см. рисунок 1), то все коэффициенты при синусоидальных составляющих будут равны нулю )  (так как под интегралом окажется нечётная функция, а интегрирование идёт в симметричных пределах). В радиотехнике отношение  называют скважностью последовательности. Окончательные выражения для коэффициентов ряда, наеденные по формуле (1.2)

где через q обозначено отклонение

Аналогично:

.

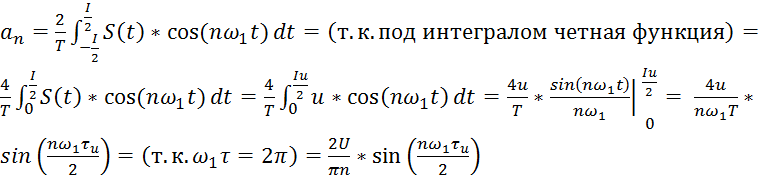Подставив выражения для коэффициентов ряда в формулу (1.1) , получим ряд Фурье для нашей последовательности видеоимпульсов нашего сигнала:

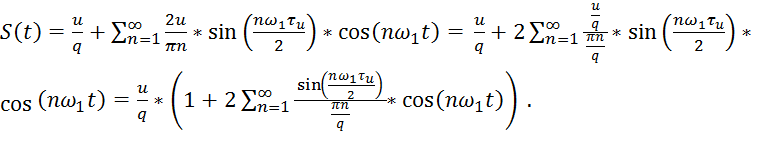          (1.3)

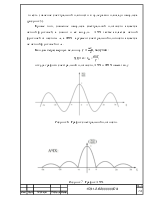
Ряд Фурье любого периодического сигнала:

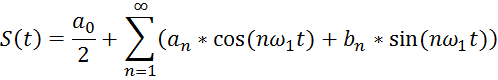
Можно преобразовать следующим образом:

 ,

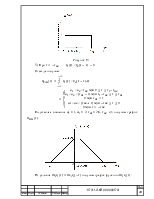
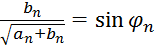 , где угол  изображён на рисунке 3 .

                                                    y

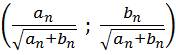
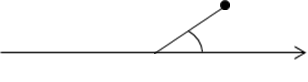Рисунок 3- Окружность с углом .

Получим:

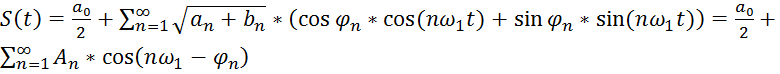, где - амплитуды соответствующих гармонических колебаний, а   -сдвиг по фазе.

Поэтому график амплитудных коэффициентов  называют амплитудным спектром, а график фазовых отклонений - фазовым спектром (см. приложение А).

Амплитудный и фазовый спектры, вместе, полностью характеризуют исходный периодический сигнал.

В нашем случае , откуда  , а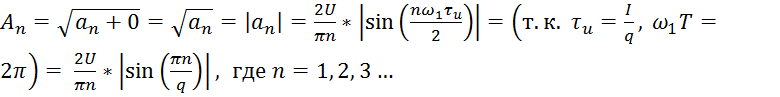  

При n=0: , т.е.  (постоянная, т.е. не зависящая от времени составляющая ряда Фурье).

При  и длительностью импульса получим значения скважности: ,

При получим значение скважности:

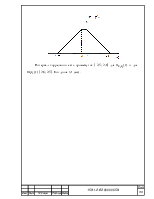
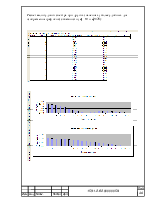
Соответственно, для первого случая получим следующее значение амплитудного спектра:

                         (1.4)

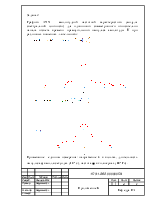
а для второго:

                        (1.5)

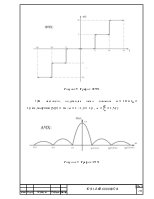
Вычисляя в Excel, получим (см. приложение А).

2)  Так как под синусом стоит величина πn/q, а период абсолютного значения синуса равен π, то получим, что количество гармонических попадающих в один лепесток спектра (ширена спектра) равна q. То есть , чем больше значение q (скважность импульса), тем больше ширина спектра. Это мы наблюдаем и на полученных графиках.

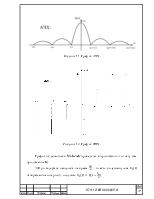
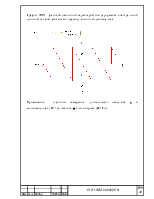
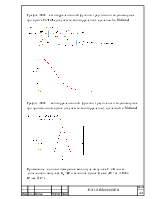
Для большей наглядности на листе 2 Excel (см. задача 1) приведены расчёты спектра для больших значениях скважности: ,а так же их графики, на которых более отчётливо видна высказанная выше зависимость (см. приложение А)