Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное
учреждения высшего профессионального образования
«Комсомольский-на-Амуре государственный
технический университет»
Электротехнический факультет
Расчетно-графическое задание
по дисциплине «Основы теории сигналов»
Вариант 3.2
Студент группы 0ПЭ
Преподаватель
2013
Содержание
|
1 |
Задача 1 |
………………………………………………………………. |
3 |
|
|
2 |
Задача 2 |
………………………………………………………………. |
8 |
|
|
3 |
Задача 3 |
………………………………………………………………. |
16 |
|
|
4 |
Задача 4 |
………………………………………………………………. |
20 |
|
|
5 |
Список использованных источников |
………………………………… |
23 |
|
Задача 1
Построить амплитудную спектральную диаграмму четной периодической
последовательности прямоугольных импульсов (рис.1, а) с длительностью ![]() и амплитудой
и амплитудой ![]() при двух значениях
периода
при двух значениях
периода ![]() и
и ![]() . Проанализировать
изменение спектра последовательности в зависимости от скважности импульсов.
Как изменится спектр рассматриваемой последовательности при совмещении начала
отсчета времени с фронтом одного из импульсов (рис. 1, б)?
. Проанализировать
изменение спектра последовательности в зависимости от скважности импульсов.
Как изменится спектр рассматриваемой последовательности при совмещении начала
отсчета времени с фронтом одного из импульсов (рис. 1, б)?
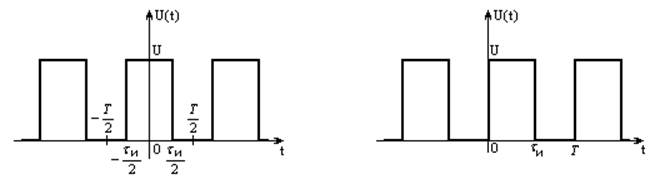
а) б)
Рисунок 1 - Четная периодическая последовательность
прямоугольных импульсов
Исходные данные: ![]() мс,
мс, ![]() В,
В, ![]() мс,
мс, ![]() мс.
мс.
Решение:
Случай 1 (рис. 1, а)
Разложим сигнал в ряд Фурье:
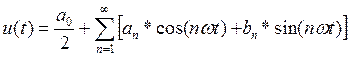 (1)
(1)
а) ![]() мс
мс
Так как сигнал u(t) симметричен (четный) относительно точки ![]() , то коэффициенты при
синусоидальных составляющих будут равны нулю (
, то коэффициенты при
синусоидальных составляющих будут равны нулю (![]() ). Обозначим отношение
). Обозначим отношение ![]() – скважность последовательности.
Найдем коэффициенты
– скважность последовательности.
Найдем коэффициенты ![]() и
и ![]() ряда Фурье по формулам:
ряда Фурье по формулам:
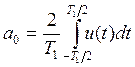 (2),
(2),
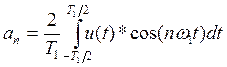 (3),
(3),
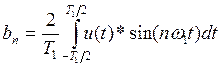 (4).
(4).
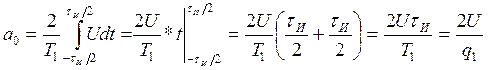
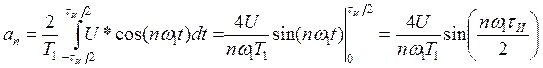
Так как ![]() , то
, то 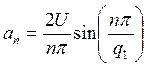
Подставив выражения для коэффициентов в формулу ряда Фурье, получим:
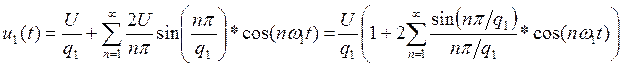 (5)
(5)
Так как коэффициенты при синусоидальных составляющих равны нулю, то амплитудный спектр последовательности будет представлен коэффициентами при косинусоидальных составляющих, взятых по абсолютному значению:
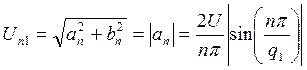 (6)
(6)
б)
![]() мс
мс
Заменяя в формулах (5) и (6) ![]() ,
, ![]() на
на ![]() ,
, ![]() , получаем разложение в
ряд Фурье и амплитудный спектр для случая б:
, получаем разложение в
ряд Фурье и амплитудный спектр для случая б:
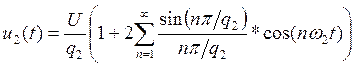
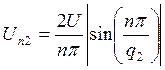
![]() ,
, ![]()
Таблица 1 – Амплитудные спектры
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
0.551 |
0.276 |
0 |
0.138 |
0.11 |
0 |
0.079 |
0.069 |
0 |
0.055 |
0.05 |
0 |
|
|
0.58 |
0.24 |
0.06 |
0.16 |
0.07 |
0.06 |
0.09 |
0.02 |
0.05 |
0.06 |
0 |
0.05 |
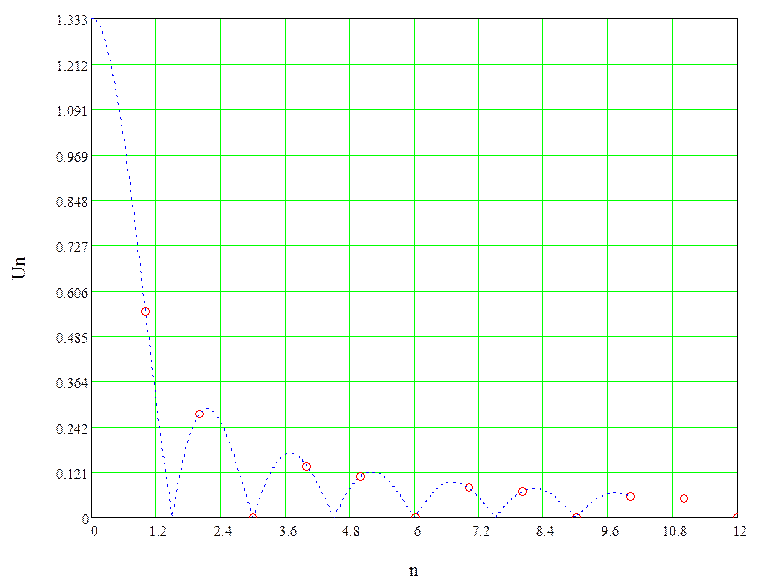
Рисунок 2 – Амплитудный спектр периодической
последовательности прямоугольных импульсов а для ![]() мс
мс
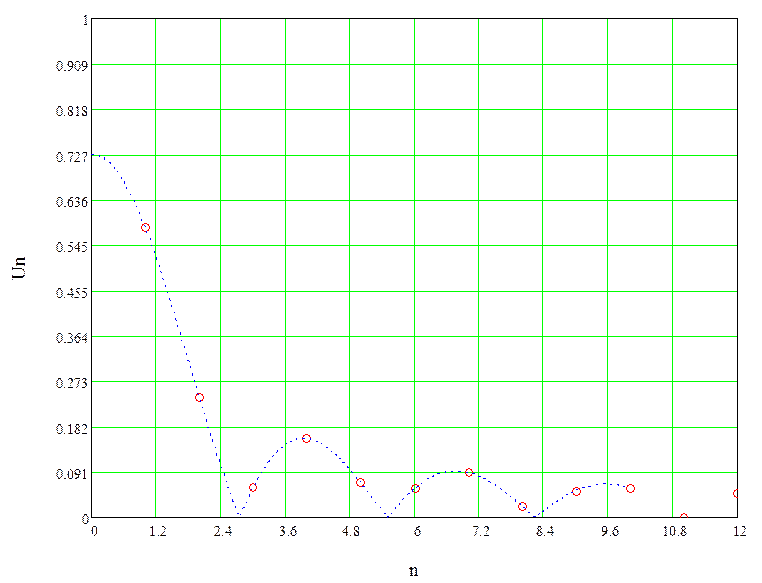 |
Рисунок 3 – Амплитудный спектр периодической
последовательности прямоугольных импульсов а для ![]() мс
мс
По графикам видно, что при увеличении скважности импульсов (периода), ширина спектра возрастает, т.е. в спектре последовательности прямоугольных импульсов наблюдается большее число гармонических составляющих. Оценим ширину основного лепестка амплитудного спектров:
а) для ![]()
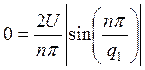 ,
, 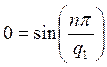 ,
, 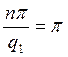 ,
, ![]()
а) для ![]()
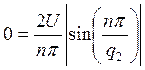 ,
, 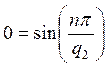 ,
, 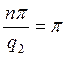 ,
, ![]()
Случай 2 (рис. 1,б)
В случае, когда начало отсчета совпадает с фронтом одного из импульсов (последовательность становится нечетной), коэффициенты ряда Фурье, стоящие при синусоидальных составляющих уже не будут равны нулю. Находим коэффициенты ряда Фурье по формулам (2), (3), (4):
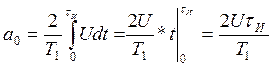
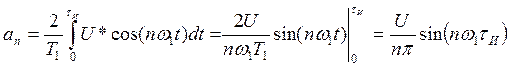
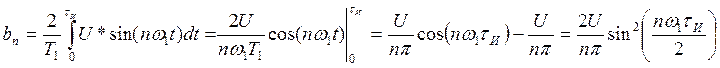
Выражение для ряда Фурье данной последовательности имеет вид:
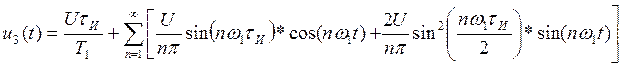
Выполним преобразования:
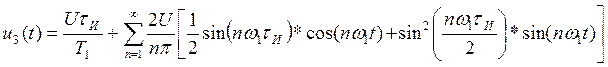
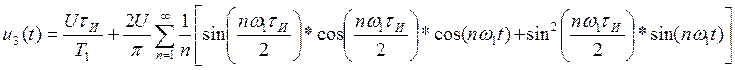
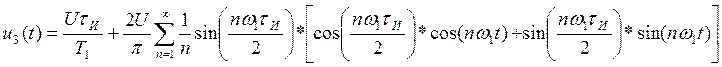
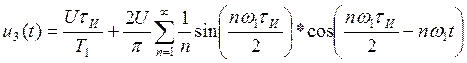
Найдем амплитудный спектр последовательности:
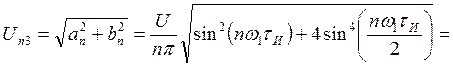
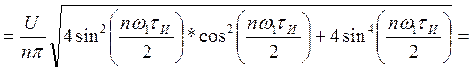
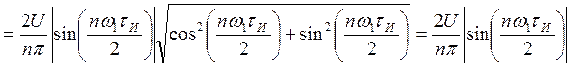
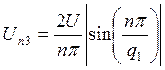
Мы видим, что при совмещении начала отсчета с фронтом одного из импульсов амплитудный спектр сигнала не изменяется.
Задача 2
Определить спектральною плотность униполярного прямоугольного импульса,
изображенного на рис.5. Построить АЧХ и ФЧХ спектральной плотности при заданных
длительности и амплитуде импульса. С использованием полученных графиков
построить аналогичные зависимости для импульсов вдвое меньшей длительности.
Отобразить на графиках влияние задержки импульса на время ![]() . Сравнить спектры
импульсной последовательности из задачи 1 и одиночного импульса. Длительность
импульса и его величина соответствуют данным задачи 1.
. Сравнить спектры
импульсной последовательности из задачи 1 и одиночного импульса. Длительность
импульса и его величина соответствуют данным задачи 1.
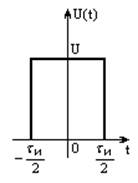
Рисунок 4 – Униполярный прямоугольный импульс
Решение:
Найдем спектральную плотность униполярного прямоугольного импульса по формуле:
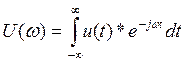 (7)
(7)
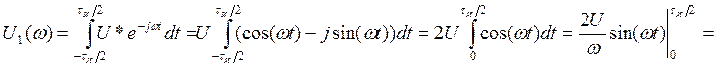
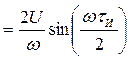
или
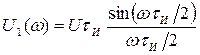 (8)
(8)
Запишем спектральную плотность униполярного прямоугольного импульса в виде:
![]() ,
,
где 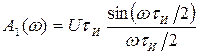 ,
, ![]() .
.
АЧХ и ФЧХ спектральной плотности определяются по формулам:
![]() ,
, 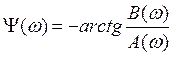
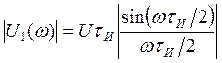 (9)
(9)
![]() (10)
(10)
Заменяя
в формулах (8), (9), (10) ![]() на
на ![]() получаем спектральную плотность, АЧХ и ФЧХ для импульса вдвое
короче:
получаем спектральную плотность, АЧХ и ФЧХ для импульса вдвое
короче:
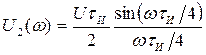
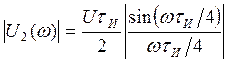
Таблица 2 - Спектральная плотность прямоугольного одиночного импульса с большей длительностью
|
|
1.6 |
1.589 |
1.558 |
1.506 |
1.435 |
0.727 |
-0.303 |
-0.745 |
0.198 |
-0.087 |
|
|
0 |
500 |
1000 |
1500 |
2000 |
5000 |
10000 |
15000 |
20000 |
25000 |
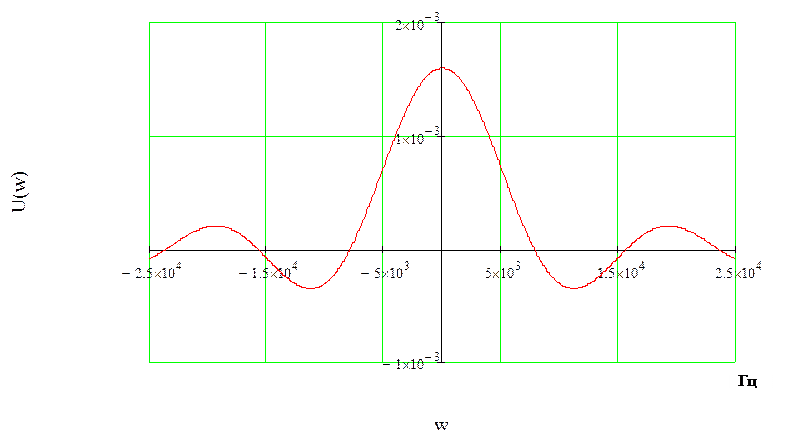
Рисунок 5 – Спектральная плотность импульса с большей длительностью
Таблица 3 - Спектральная плотность прямоугольного одиночного импульса с меньшей длительностью
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.