Амплитудная спектральная диаграмма четной периодической последовательности прямоугольных импульсов, страница 2

	0.8	0.795	0.753	0.673	0.364	0.0376	-0.151	-0.153	-0.037	0.075
	0	1000	3000	5000	10000	15000	20000	25000	30000	35000

	Гц

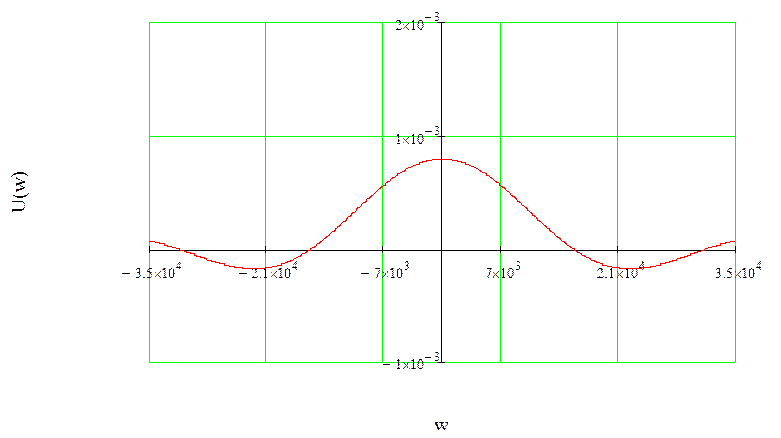
Рисунок 6 – Спектральная плотность импульса с меньшей длительностью

Таблица 4 - АЧХ прямоугольного одиночного импульса с большей длительностью

	1.6	1.558	0.727	0.303	0.745	0.198	0.087	0.0715	0.113	0.0288
	0	1000	5000	10000	15000	20000	25000	30000	350000	40000

 

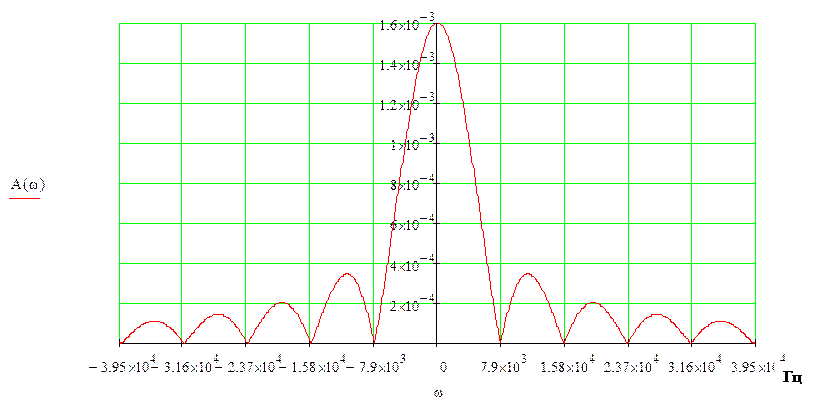
Рисунок 7 – АЧХ спектральной плотности импульса

с большей длительностью

Таблица 5 - АЧХ прямоугольного одиночного импульса с меньшей длительностью

	0.8	0.795	0.673	0.364	0.0376	0.151	0.153	0.0373	0.075	0.0989
	0	1000	5000	10000	15000	20000	25000	30000	350000	40000

 

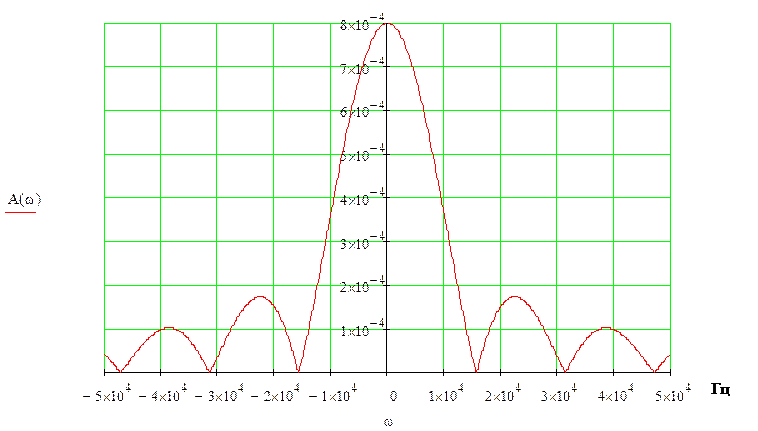Рисунок 8 – АЧХ спектральной плотности импульса

с меньшей длительностью

Таблица 6 - ФЧХ прямоугольного одиночного импульса с большей длительностью

	12,6	9,42	6,28	3,14	0	-3,14	-6,28	-9,42	-12,6
	-31600	-23700	-15800	-7900	0	7900	15800	23700	31600

 

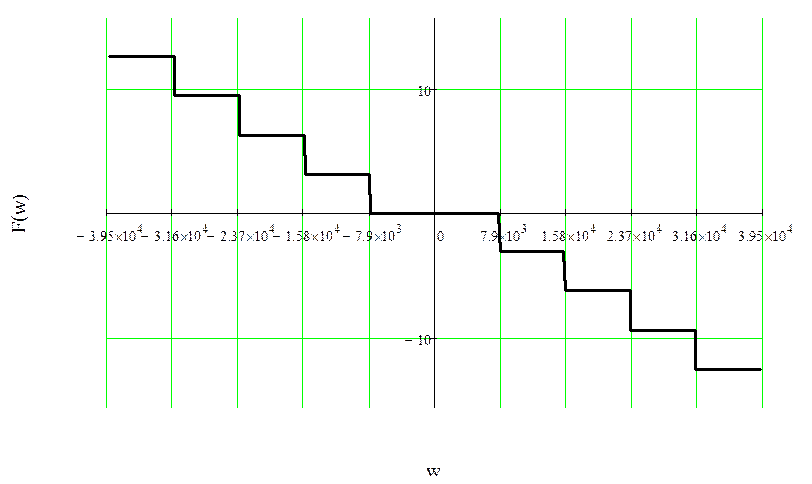
Рисунок 9 – ФЧХ спектральной плотности импульса

с большей длительностью

Таблица 7 - ФЧХ прямоугольного одиночного импульса с меньшей длительностью

	9,42	6,28	3,14	0	-3,14	-6,28	-9,42
	-47124	-31480	-15790	0	15790	31480	47124

 

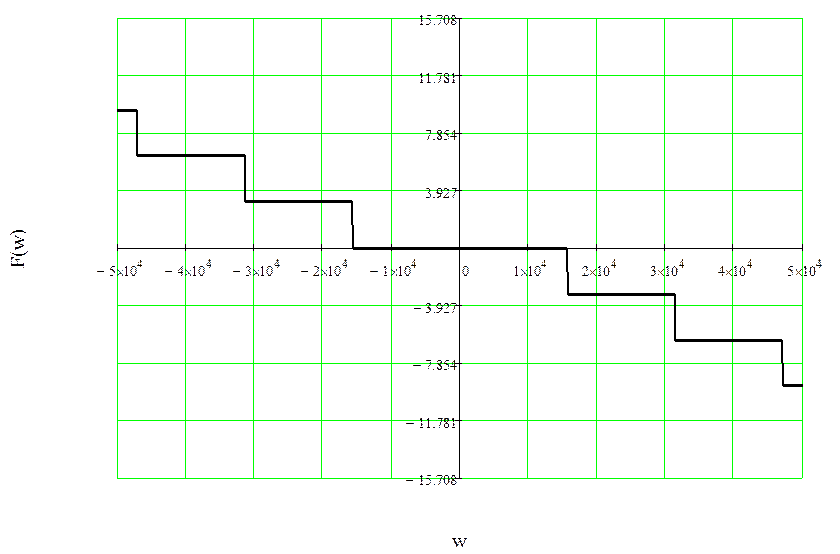
Рисунок 10 – ФЧХ спектральной плотности импульса с меньшей длительностью

Найдем спектральную плотность в случае задержки импульса на  по формуле:

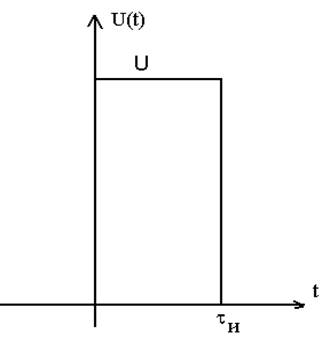
Рисунок 11 – униполярный прямоугольный импульс смещенный во времени

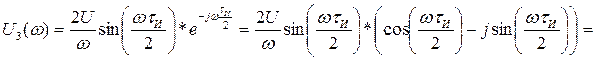
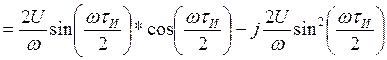
или ,

где , .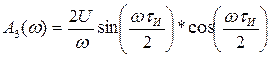

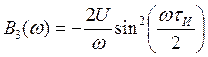Найдем АЧХ и ФЧХ полученной спектральной плотности:

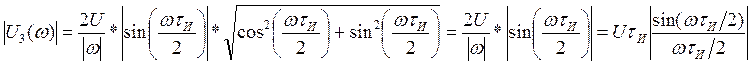
АЧХ при задержке импульса на  не изменяется.

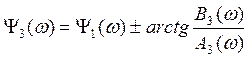
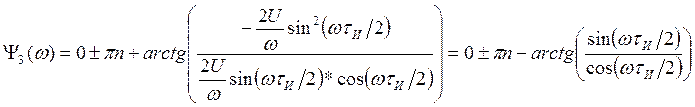
Таблица 8 - ФЧХ прямоугольного одиночного импульса смещенного на время

	25,13	18,85	6,28	6,28	0	-6,28	-12,56	-18,85	-25,13
	-31420	-23570	-15708	-7855	0	7855	15708	23570	31420

 

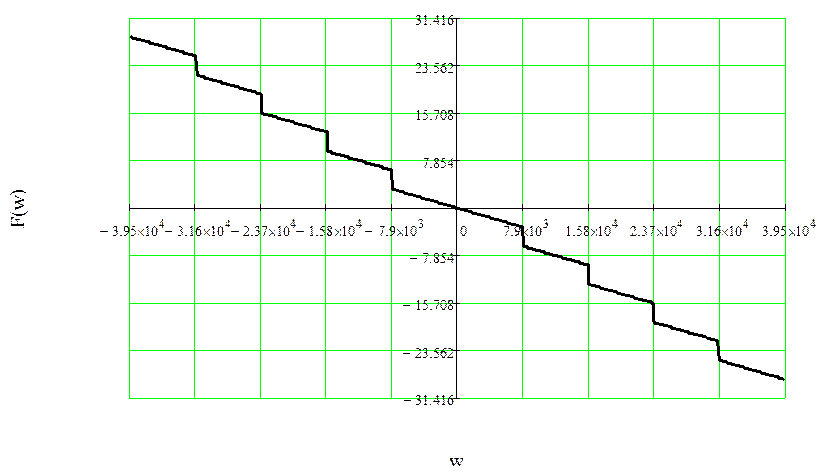
Рисунок 12 – ФЧХ спектральной плотности импульса

смещенного на время

Как видим, смещение сигнала во времени отражается лишь на   изменении фазового спектра сигнала.

Задача 3

Найти корреляционную функцию  треугольного импульса длительностью , с амплитудой  (рис.9). Определить энергию импульса, выделяемую на сопротивлении 1 Ом. Построить график функции. Данные по длительности и величине импульса соответствуют данным задачи 1.

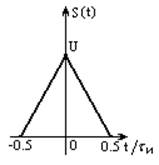
Рисунок 13 – Треугольный импульс

Решение:

Автокорреляционная функция (АКФ) сигнала определяется по формуле:

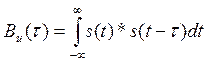  (11)

Математическая модель треугольного сигнала имеет вид:

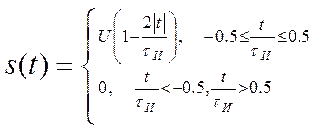
Для нахождения АКФ треугольного импульса необходимо выполнить элементарные построения (рис. 13).

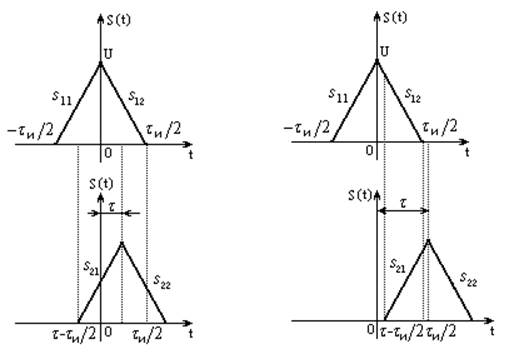
а)                                            б)

Рисунок 14 – Взаимное расположение импульсов:

а) 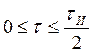; б)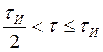

Введем вспомогательные функции:

, ,

,

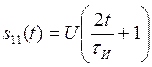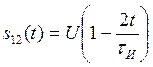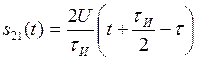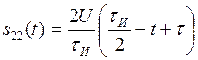
Для случая а) АКФ определится суммой трех интегралов:

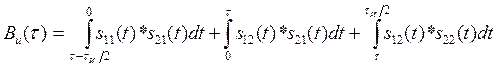
Посчитаем интегралы отдельно:

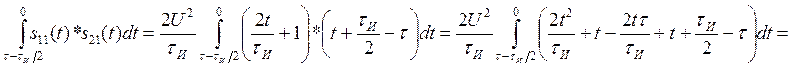
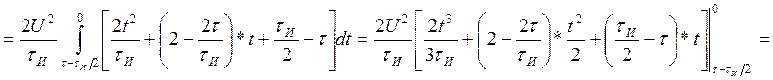
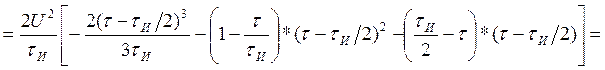
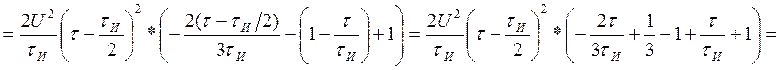
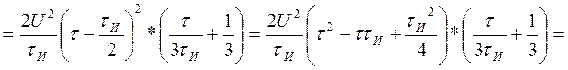
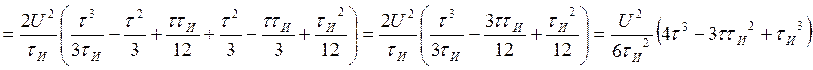
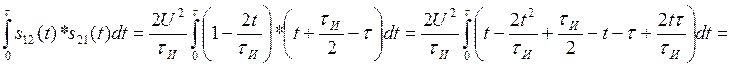
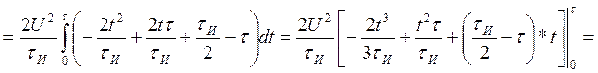
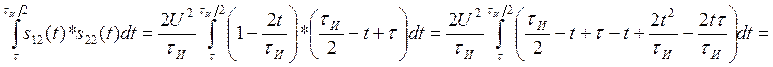
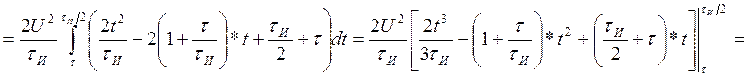
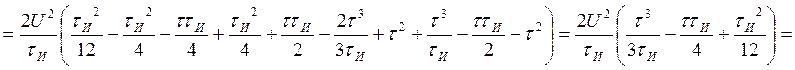
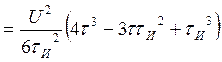
Находим АКФ:

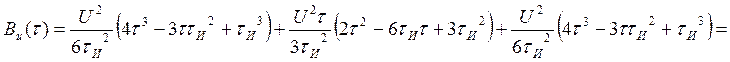
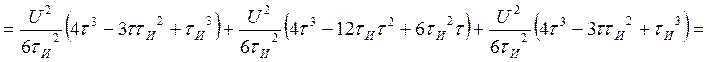
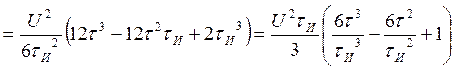
Для случая б) АКФ:

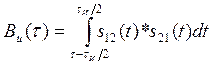
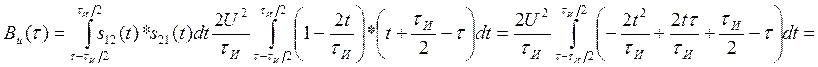
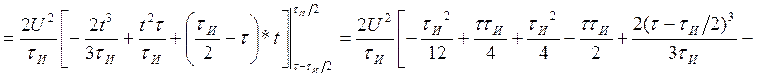
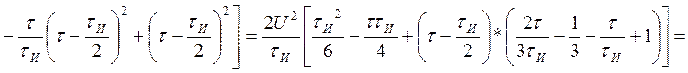
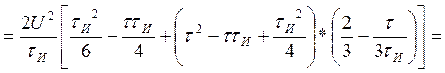
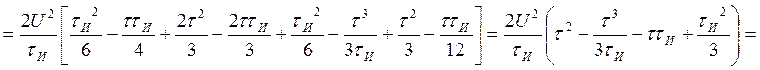
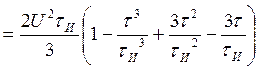
Объединяя оба случая, получаем выражение для АКФ:

                               

          

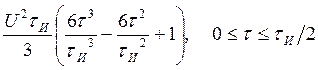
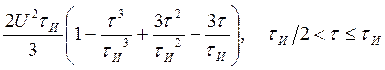
В области   .

Найдем энергию сигнала:

,              

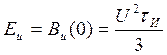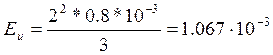
Таблица 9 – АКФ сигнала треугольной формы

Bu(t)∙10-3	1.067	0.979	0.767	0.504	0.267	0.113	0.033	0.00417	0
t∙10-3	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8

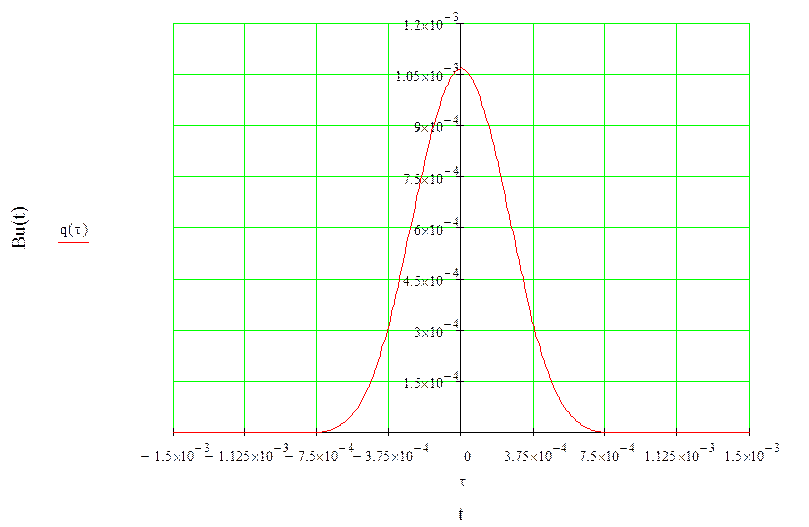
Рисунок 15 – АКФ сигнала треугольной формы

Задача 4

Найти взаимную корреляционную функцию двух прямоугольных импульсов с параметрами , , , (рис. 14). Определить интервал корреляции.

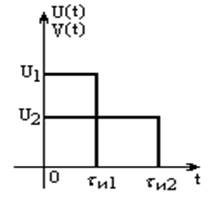
Рисунок 16 – Два прямоугольных импульса

Исходные данные:  В, мс,  В,  мс.

Решение:

Изобразим возможные варианты расположения двух импульсов:

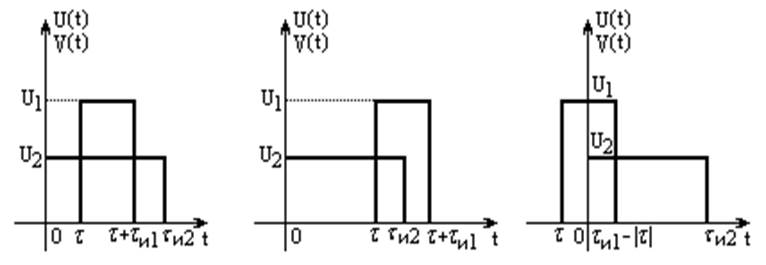
а)                                        б)                                       в)

Рисунок 17 – Варианты взаимного расположения импульсов.

Взаимокорреляционная функция (ВКФ) определяется по формуле:

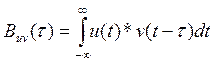  (12)

Для случая а):

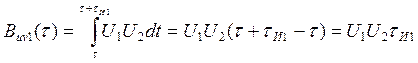
Для случая б):

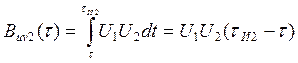
Для случая в):

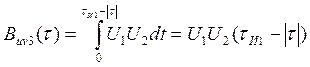
Объединяя три случая, получаем выражение для ВКФ двух прямоугольных импульсов:

                               

          

 

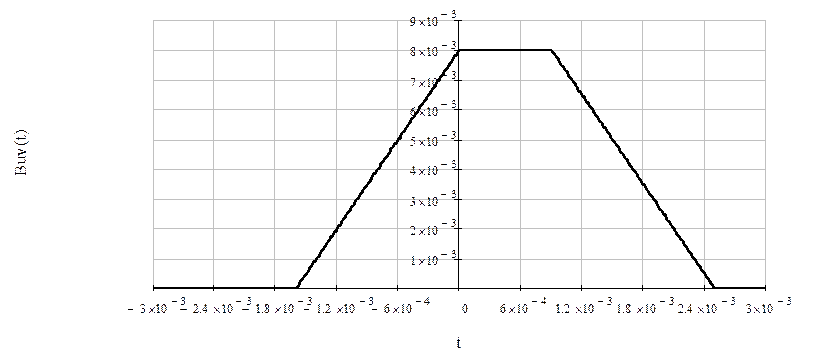
Рисунок 18 – ВКФ двух прямоугольных импульсов.

τ_к=1,586*10^-3 с.

Список использованных источников

1. Баскаков С.И. Радиотехнические цепи и сигналы. М.: Высшая школа. 2000. -462 с.

2. Баскаков С.И. Радиотехнические цепи и сигналы. Руководство к решению задач. М.: Высшая школа. 2002. - 214 с.