Амплитудная спектральная диаграмма чётной периодической последовательности прямоугольных импульсов, страница 2

При малых же значениях скважности (тем более дробных, как при значениях  , , полученных по данным варианта), эта картина не так отчётлива (так если при в лепесток спектра попадет приближенно одна гармоника, то при  – приближённо две гармоники, что не даёт возможность наглядно увидеть характер спектра, хотя и просматривается, но не так отчётливо, как при больших значениях q).

3)  Для того чтобы получить ряд Фурье для сигнала на рисунке 2 см. условие задачи), рассмотрим сигнал  .

Он будет иметь вид, изображённый на рисунке 4, продолженным нечётным образом с отрезка . (Исходный сигнал имел амплитуду U на отрезке и равнялся 0 на отрезке ; у нашего: амплитуда на отрезке  и  на отрезке ; далее оба продолжались периодическим образом с периодом Т).

                                                   U(t)

                                         

                                                                       T

0                                                    t

                                        

Рисунок 4 - Сигнал продолженный нечётным образом на отрезке [0; Т].

Исходный сигнал имел амплитуду U на отрезке и равнялся 0 на отрезке ; у нашего: амплитуда на отрезке  и  на отрезке ; далее оба продолжались периодическим образом с периодом Т

Исправленный сигнал  хорош тем, что  это нечётная функция, а значит все (включая) равны нулю. Коэффициенты  ряда Фурье вычисляется по формулам:

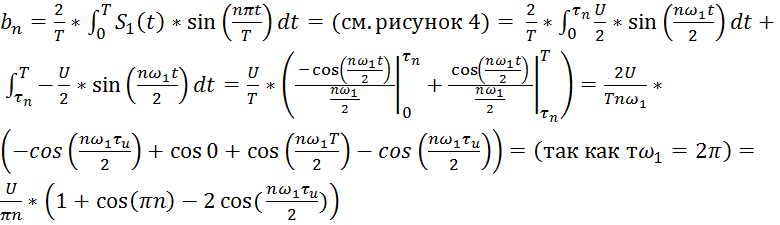                                                    (1.6)

Так как 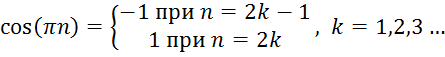 , то получим:

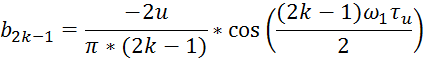
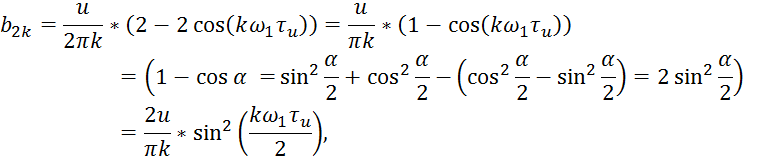
Итак, исправленный сигнал  имеет следующий ряд Фурье:

 , где коэффициент  вычисляется по формуле (1.6), а значит исходный сигнал , изображённый на рисунке 2, будет иметь следующий ряд Фурье:

 , где  ,

 так же вычисляется по формуле (1.6).

Так как , то можно записать разложение сигнала  в классическом виде:

,

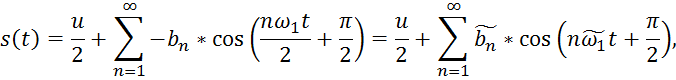
 , то есть амплитуды гармоник , а фазовый спектр постоянной: ;

В роли основной частоты выступает  . Расчёты проводим в Excel

(см. приложение А)

Определить спектральную плотность прямоугольного видеоимпульса, изображённого на рисунке 5, .

1)  Построить амплитудную (АЧХ) и фазовую (ФЧХ) частотные характеристики при фазовых значениях длительности .

2)  С использованием полученных графиков построить АЧХ и ФЧХ для импульса в двое меньше длительности.

3)  Отобразить на графиках влияние задержки импульса на время .

4)  Сравнить спектры импульсной последовательности из задания 1 и одиночного импульса.

                                                              U(t)

U

 

t

                        

Рисунок 5- Одиночный прямоугольный видеоимпульс.

Решение:

Для решения данной задачи необходимо внимательно изучить материал параграфа 2.2 учебного пособия [5] . Спектральная плотность сигнала задаётся его преобразование Фурье:

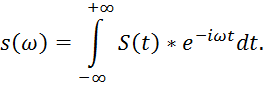
В нашем случае получим:

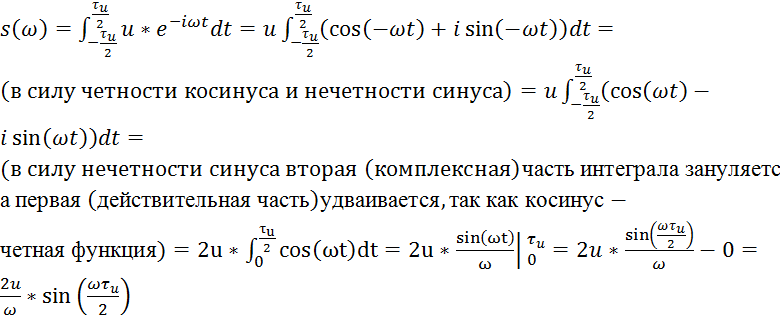                                        (2.1)

Итак, спектральная плотность прямоугольного видеоимпульса  является действительной функцией (комплексная часть нулевая). Но и в случае нулевой и комплексной части фазовый спектр определяют аналогично общему случаю:

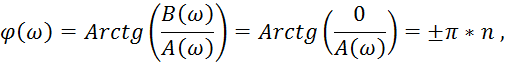
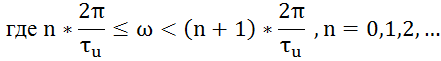
Здесь  – действительная и мнимая части комплексной спектральной плотности:

                            (2.2)

Отметим, что:

,

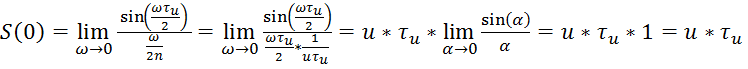то есть значение спектральной плотности в нуле равно площади импульса (рисунок 5).

Кроме того, значение импульса спектральной плотности является чётной функцией, а значит и её модуль - АЧХ также является чётной функцией от частоты , а ФЧХ- аргумент спектральной плотности является не чётной функцией от .

Вводим безразмерную величину

, откуда графики спектральной плотности, АЧХ и ФЧХ имеют вид: