Амплитудная спектральная диаграмма чётной периодической последовательности прямоугольных импульсов, страница 4

График АКФ рассчитанный в Exсel и Mathcad прилагается (см. приложение В).

При   даёт энергию сигнала, т.к. .

Сделаем ещё одну проверку вычислений, непосредственно посчитав .

Имеем:

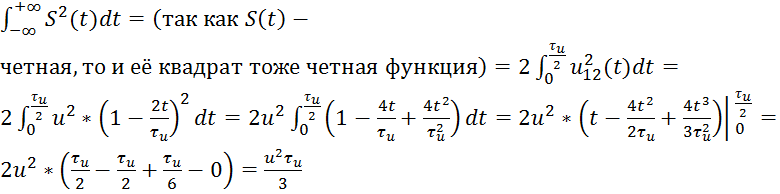, что совпадает с .

Итак, энергия импульса выделяется на сопротивлении 1 Ом (энергия сигнала) равна:

 .

 

Найти взаимную корреляционную функцию двух прямоугольных импульсов (см. рис. ) с параметрами u₁ = 1 В, τ_u1 = 2,6 мс, u₂ = 2 В, τ_u2 = 2,5 мс.

Определить интервал корреляции.

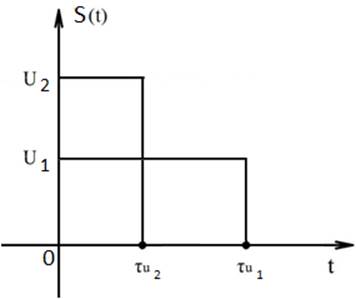
Рисунок 16 Решение:

Взаимокорреляционная функция двух сигналов S₁ (t) и S₂(t) определяется формулой:

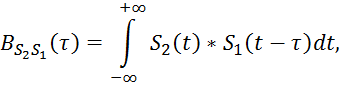
Соответственно:

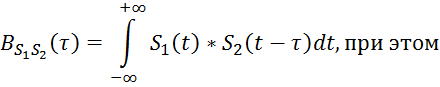
, так что, достаточно найти одну из них.

В нашем случае:

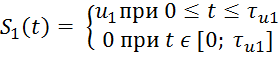
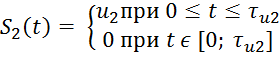
Поэтому получим:

1)  При

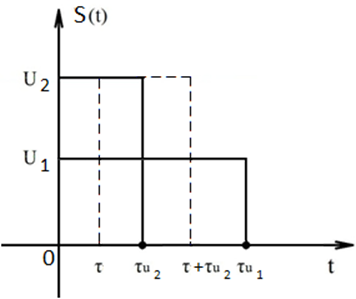
Рисунок 17 -

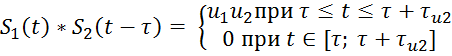
2)  При

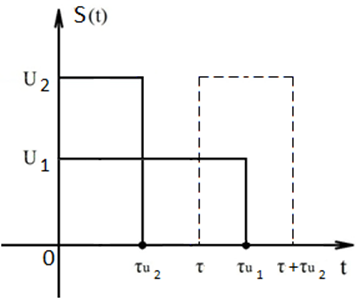
Рисунок 18 -

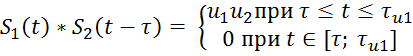
3)  При     

4)  При

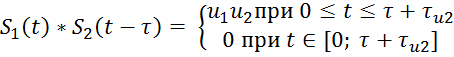
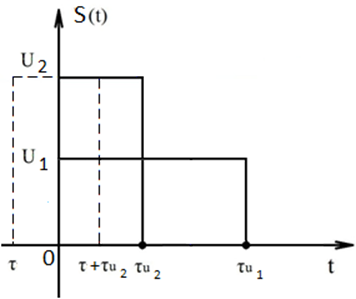
Рисунок 19 5)  При        

Отсюда получим:

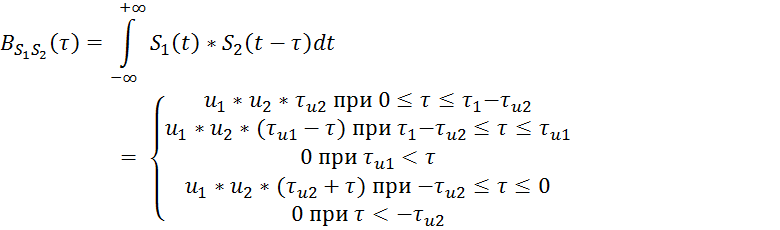
Подставляя значения u₁ = 1, u₂ = 2, = 2,6, =2,5 получим график

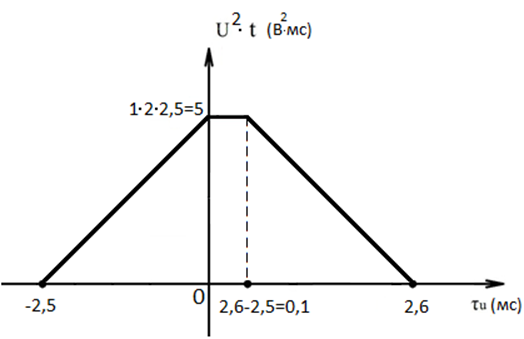
Из условия  получим график функции

Интервал корреляции есть промежуток [-2,5; 2,6] для  и для [-2,6; 2,5]. Его длина 5,1 (мс).

 

Для схемы (см. рисунок 16) определить частотный коэффициент передачи линейной стационарной системы, построить графики АЧХ и ФЧХ. Определить реакцию системы на дельта- функцию, построить график импульсной характеристики системы.

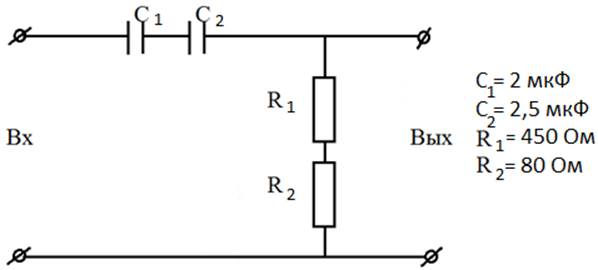
Рисунок 20- Схема.

Решение:

1)  Для решения данной задачи вспомним некоторые основные положения.

Важнейшей характеристикой линейной стационарной системы (ЛСС) является h(t)- импульсная характеристика системы, которая определяется как реакция системы на мгновенный импульс единственной мощности, то есть формулой:

, где  -дельта функция Дирака,

 – оператор системы.

В силу линейности и принципа суперпозиции, зная h(t) можно найти реакцию системы на любой входной сигнал посредством интеграла Дюамеля:

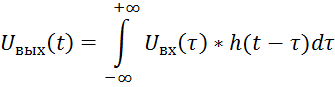
 (т.е. как свёртку входного сигнала с импульсной характеристикой системы h(t)).

Или (с учётом физической реализации, то есть условия: h(t)=0 при t<0):

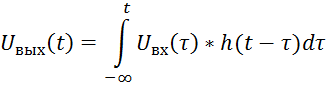
Особый интерес представляют такие сигналы, которые проходя через ЛСС не меняются по форме, а лишь масштабируются, то есть которых выполняется равенство:

Такие сигналы называются собственными функциями ЛСС, а λ- собственным числом оператора Т.

Комплексный сигнал вида  при любом значении частоты  является собственной функцией любой ЛСС, так как используя свёртку (интеграл Дюамеля) получим:

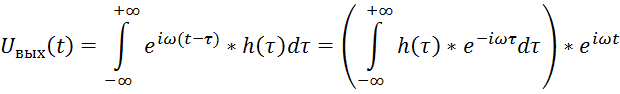
Из последнего равенства следует, что собственным значением оператора ЛСС является комплексное число:

, называемое частотным коэффициентом передачи системы.

Так как  является преобразованием Фурье импульсной характеристики системы, то импульсная характеристика системы h(t) может быть найден через  с помощью обратного преобразование Фурье:

.

2)Перейдём к расчётам нашей ЛСС. Из конкретного вида ЛСС (см. рисунок 16), так как через конденсаторы с емкостями С₁ и С₂ и сопротивления R₁ и R₂  идет ток I, получим:

,

 ,

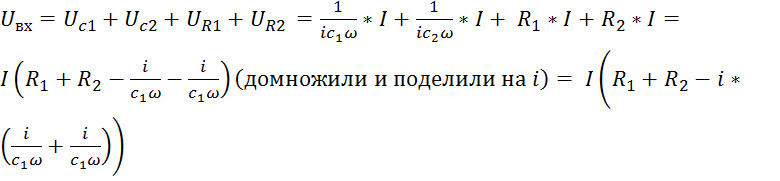Откуда:

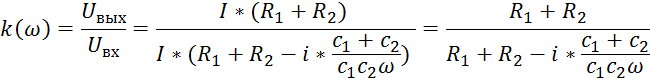
Итак, частотный коэффициент передачи нашей ЛСС имеет вид 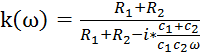 и выражает, во сколько раз изменяется подаваемый гармонический сигнал  при каждом значении частоты .

3) Так как -число, вообще говоря, комплексное, то выделяют его модуль  , называемый АЧХ – амплитудой частотной характеристикой ЛСС (и показывающий во сколько раз изменится амплитуда входного сигнала) и аргумент , называемый ФЧХ- фазовой частотной характеристикой ЛСС (показывающей как изменяется фаза при прохождении входного гармонического сигнала через систему).

4)В нашем случае:

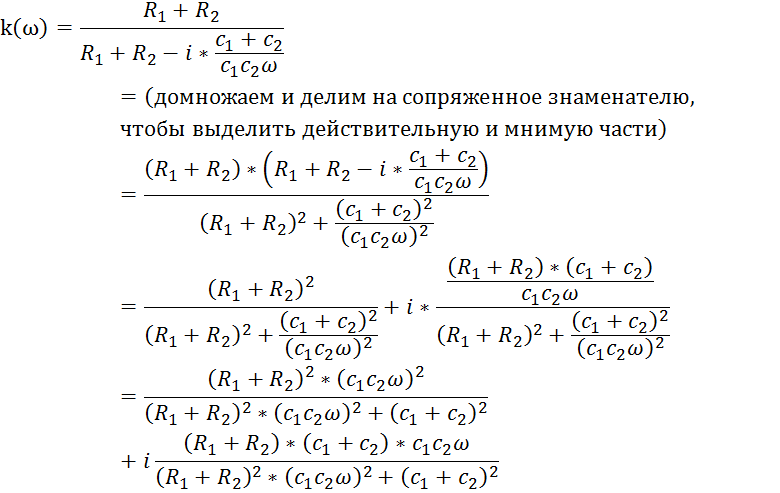
Откуда:

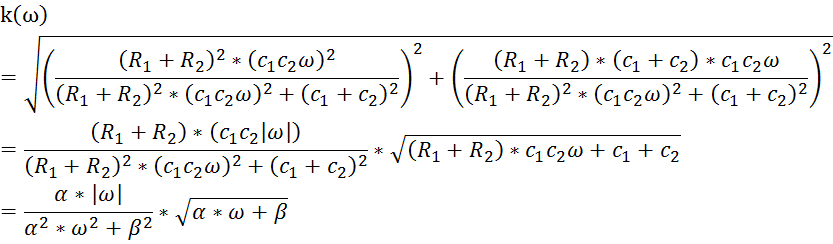
где

Подставляя  значения      строим её график в Mathcad (см. приложение Г).

5)Найдём ФЧХ системы, то есть .