Амплитудная спектральная диаграмма чётной периодической последовательности прямоугольных импульсов, страница 3

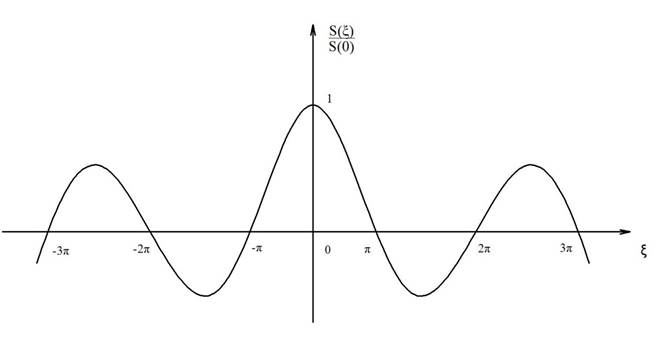
Рисунок 6- График спектральной плотности.

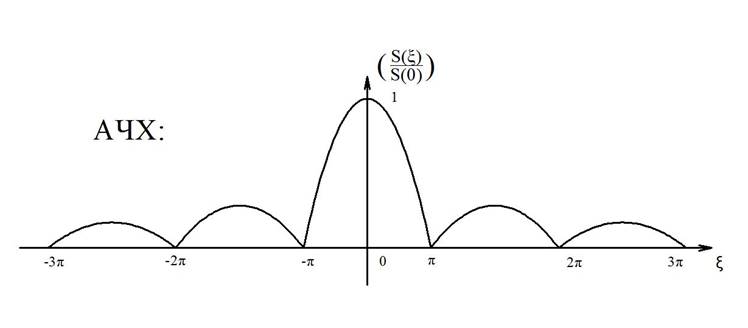
Рисунок 7- График АЧХ.

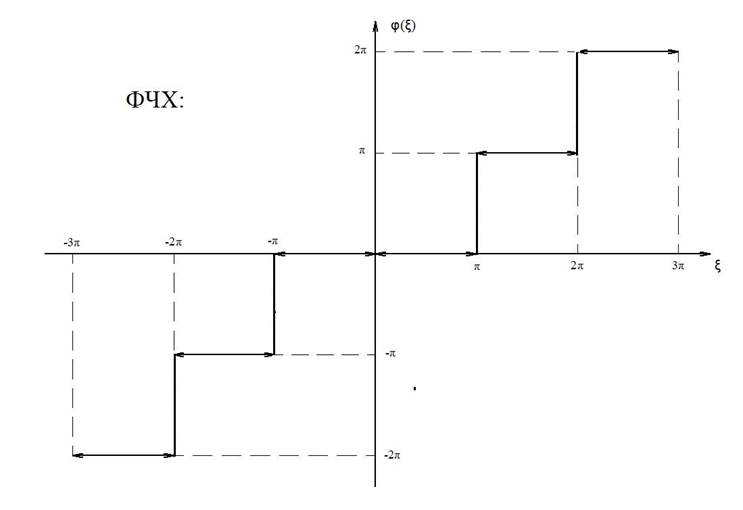
Рисунок 8- График  ФЧХ.

1) В частности, подставляя наши значения ):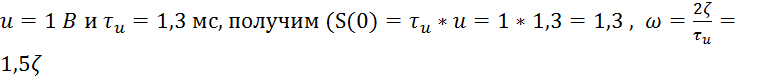

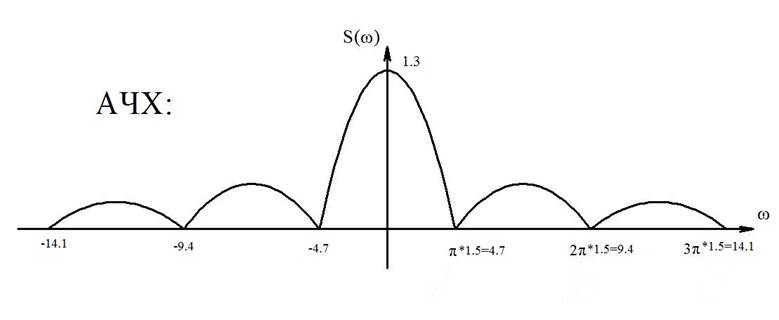
Рисунок 9- График АЧХ.

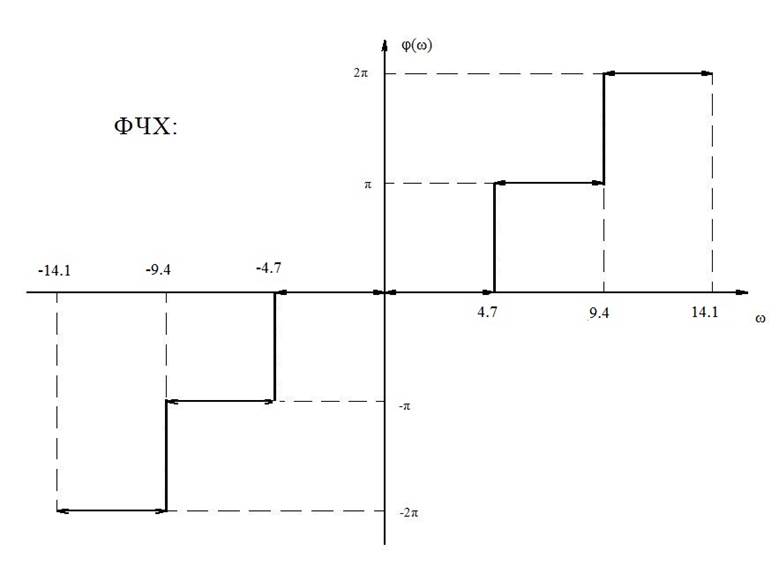
Рисунок 10- График ФЧХ.

2) При  получим, что  уменьшится вдвое, а  увеличивается вдвое, то есть графики АЧХ и ФЧХ видеоимпульса вдвое меньше длительности (и той же амплитуды) примут вид (амплитуда спектра уменьшится вдвое, а ширина спектра расширится):

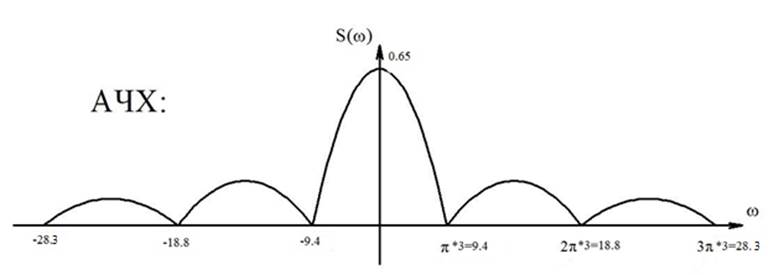
Рисунок 11- График АЧХ.

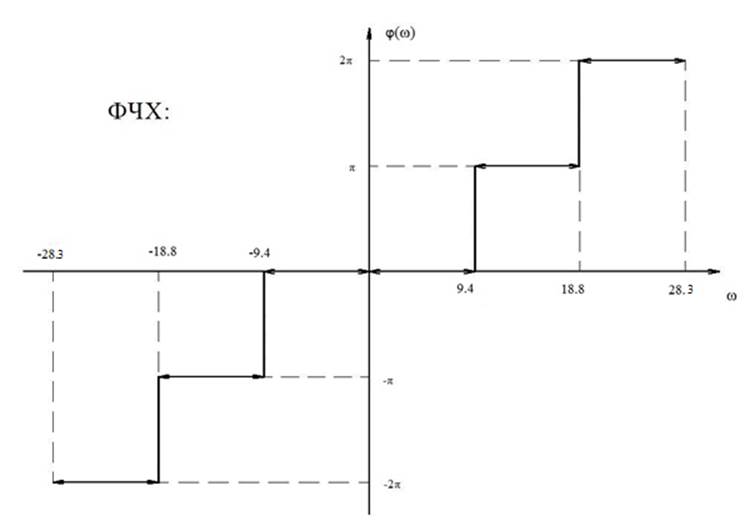
Рисунок 12- График ФЧХ.

Графики сделанные в Mathcade приведены в приложении к отчёту (см. приложение Б).

3)  При задержке импульса на время  , то есть видеоимпульса  изображённого на рис.5 , получим: :

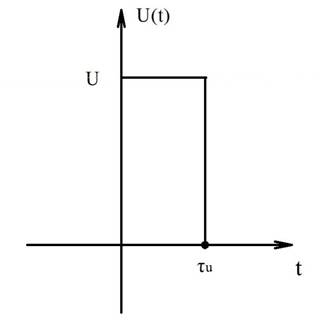
Рисунок 13- Видеоимпульс .

Отсюда получим для спектральной плотности (преобразование Фурье) сигнала :

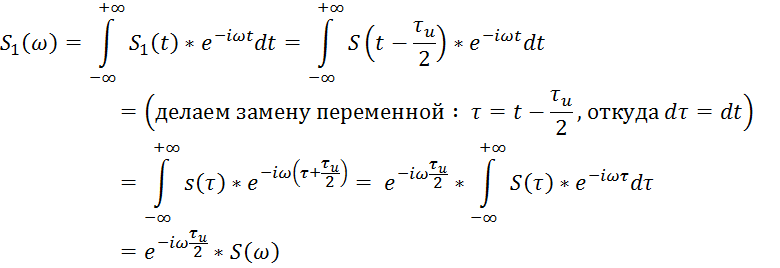
Таким образом, спектральная плотность симметричного видеоимпульса  при его запаздывании на  , то есть для видеоимпульса  умножается на функцию .

Так как 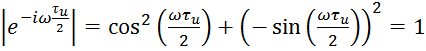 , то амплитудная фазовая характеристика при его запаздывании на любое время не изменяется  , а вот фазовый спектр (аргумент спектральной плотности изменится) действительно имеет:

.

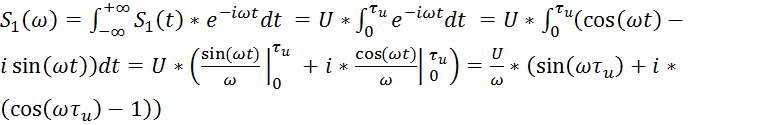Итак:

 , где  ,

.

Отсюда убедимся в независимости АЧХ:

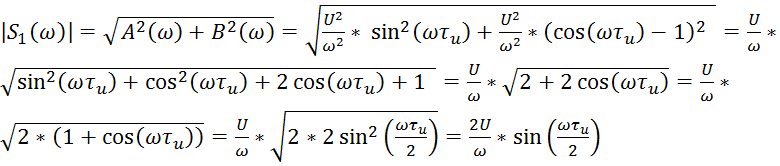, что совпадает с АЧХ для S(t).

Найдём выражение для ФЧХ:

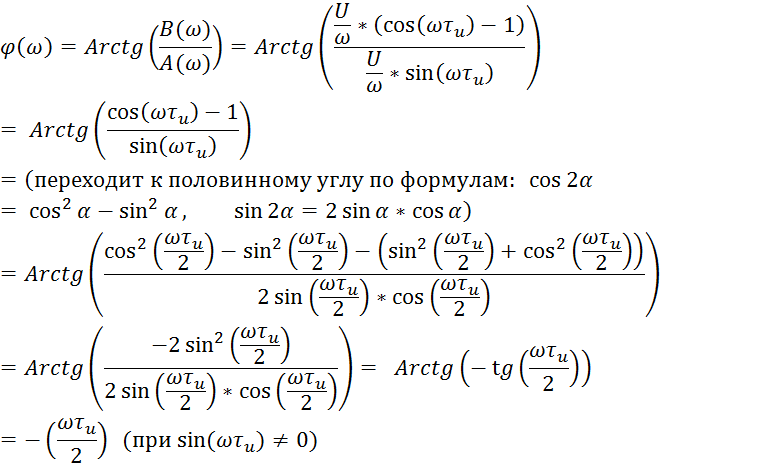
То есть ФЧХ является линейной функцией от , где она совершает скачок от значения  .

График ФЧХ  сделанный в  Mathcade , приведён в приложении к отчёту(см. приложение Б).

Заметим, что точки пересечение от частот  совпадает с точками «перескока» графика ФЧХ исходного симметричного видеоимпульса.

Видим, что ФЧХ не зависит от амплитуды U видеоимпульса, а зависит лишь от его длительности .

4)  Сравнивая спектры импульсной последовательности из задания 1 и одиночного импульса (симметричный случай) видим, что с увеличением периода Т (а значит и скважности  при фиксированной длительности), график спектра периодической функции (последовательности импульсов) приближается к графику спектральной плотности одиночного импульса (как и должно быть по теории).

1) Найти автокорреляционную функцию  треугольного видеоимпульса длительностью  (рисунок 14).

2)  Определить энергию импульса, выделяемую на сопротивлении 1 Ом.

3)  Построить график функции.

Данные по длительности и величине импульса соответствует данным задачи 1.

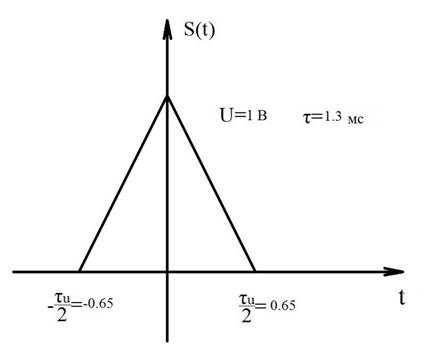
Рисунок 14- График треугольного импульса.

Решение:

Для решения данной задачи необходимо изучить теоритический материал раздела 3 (литература [1, 4, 5]), осмыслить понятия автокорреляционной функции сигнала и запомнить формулу для её определения.

1)  Автокорреляционная функция  произвольного сигнала S(t) определяет степень отличия исходного сигнала S(t) от его смещённой копии во времени S(t-) и определяется по формуле:

,

(скалярное произведение сигнала и его смещенной на τ копии).

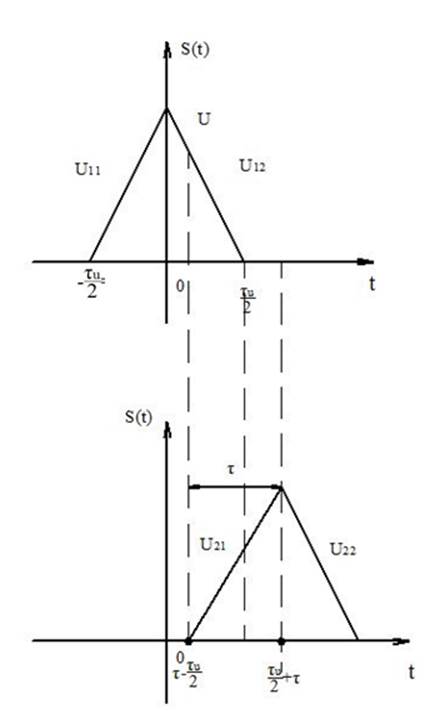
Исходный треугольный импульс можно записать следующим образом:

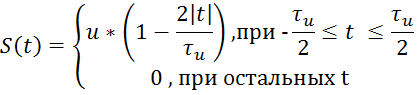
Так как по свойству автокорреляционной функции (АКФ)  (для любого сигнала), то достаточно построить её при . При этом, для нашего сигнала- треугольного импульса, принудительного различны два случая:   (при  интеграл очевидно равен нулю, то есть ).

Введём вспомогательные функции:

,

,

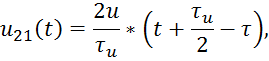
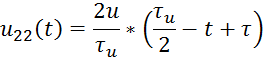
получим для случая :

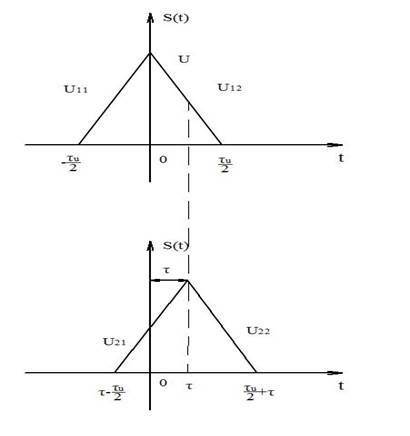
Рисунок 15- График треугольного импульса 1.

Откуда АКФ определится суммой трёх интегралов:

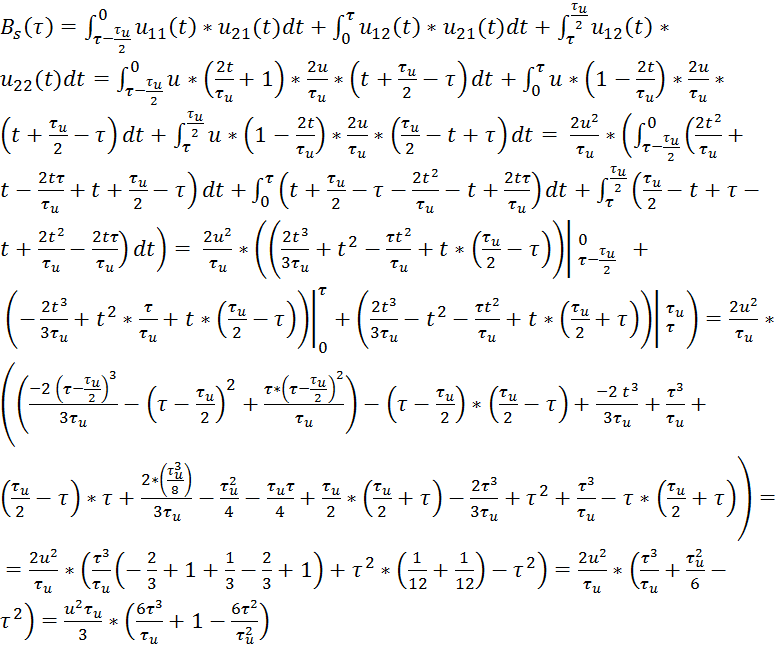
Итак, при  автокорреляционная функция АКФ имеет вид:

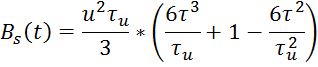
При  :

При :

При  получим:

Откуда:

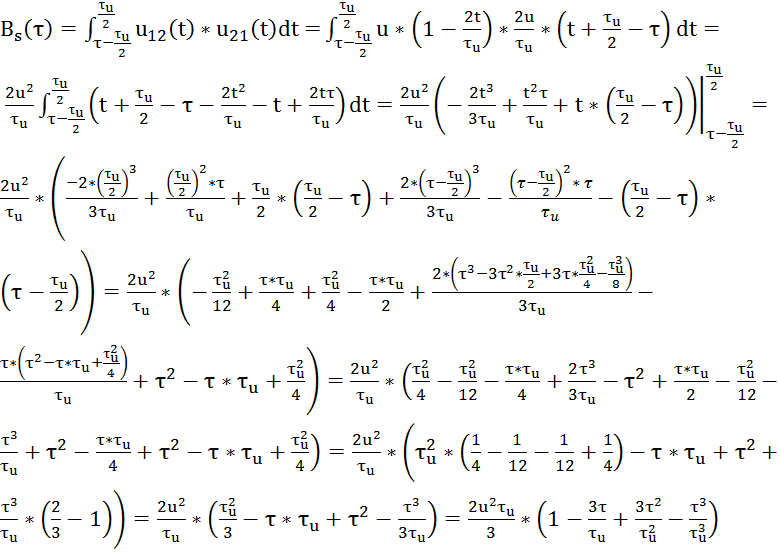
Объединяя оба случая получаем окончательный вид АКФ треугольного видеоимпульса:

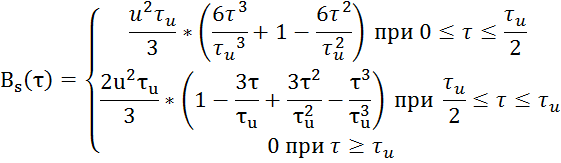
Заметим, что при  значение , посчитанное по второму случаю, так же даёт величину  (что и по первому случаю), а при  получаем 0, что подтверждает правильность расчётов (т.к. функция  в точках «стыка» должна быть непрерывной).