Проектирование производства земляных работ. Часть 1 (Распределение земляных масс. Способы разработки грунтов): Методические указания к курсовому и дипломному проектированию, страница 3

Прибавляя к строкам матрицы С числа -3, -4, -3, а к столбцам числа +1, 0, +1, -1, превратим ее в матрицу:

C₁ =

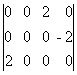
Если бы все элементы матрицы С₁ были неотрицательными, перво­начальный выбор назначений давал бы оптимальное решение. Но посколь­ку в нашем случае дело обстоит не так, то применяется процедура исправ­ления начальных назначений. Для исправления присоединяем к уже выде­ленным элементам матрицы C₁ее наибольший по абсолютной величине отрицательный элемент (в данном случае элемент С₂₄ = -2). Если началь­ный выбор содержал точно т + п — 1 элементов, то (это нетрудно дока­зать) при таком присоединении обязательно образуется цикл из выделенн­ых элементов - в данном случае цикл  (С₂₄ = -2, С₃₄ = -2, С₂₂ = 0, С₂₄).

Рассмотрим теперь соответствующий цикл

P₀ = P₂₄,  P₃₄, P₃₂, P₂₂, P₂₄

в матрице планов Р и превратим его в цикл

P₂₄ +P,  P₃₄-P, P₃₂+P, P₂₂-P, P₂₄+P

где р - наименьшая величина в четном полуцикле (P₃₄, P₂₂) цикла ро (величина р как бы сдвигается го каждого элемента четного полуцикла к следующему за ним элементу нечетного полуцикла). В нашем случае P=P₃₄=5. Производя указанное преобразование цикла и исключая из числа выделенных элементов вновь возникший нулевой элемент P₃₄-P, получим новую матрицу планов Р₁:

P₁ =

Здесь, как и раньше, полужирным шрифтом даны выделенные элементы. Выделяя те же элементы в матрице C₁, получаем матрицу  :

 =

Прибавляя к последнему столбцу число +2, приведем матрицу  к виду:

C₂ =

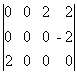
с нулевыми выделенными элементами, не содержащую отрицательных элементов. Это означает, что план P₁ оптимален. Суммарная стоимость перевозок S₁ по этому плану равна:

S₁ = 10-2 + 5-3 + 5-4 + 5-3 + 10-3 + 10-2 = 120,

в то время как суммарная стоимость перевозок S₀ по начальному плану P₀ была равна

So - 10-2 + 5-3 + 10-4 + 5-3 + 10-2 + 5-4 = 130.

Как и всякая задача линейного программирования, транспортная задача может иногда иметь не один, а множество оптимальных планов. На такую си­туацию указывает наличие дополнительных (помимо выделенных) нулей в заключительной (преобразованной) матрице удельных стоимостей. Присое­диняя эти нули точно так же, как мы поступали с отрицательными элемента­ми, можно двигать вдоль возникающих циклов то или иное количество гру­зов, не нарушая при этом оптимальности плана. Например, в заключительной матрице Сг рассмотренного выше примера можно образовать цикл из нуле­вых элементов (С₂₁, С₂₂, С₁₂, С_11, С₂₁) и передвинуть в нем какую-нибудь вели­чину груза, скажем С_22. В результате получим новый план

 =

с общей стоимостью перевозок

S₁ = 7-2 + 3-3 + 8-3 + 2-3 + 5-3 + 10-3 + Ю-2 = 120.

Таким образом, этот план, как и план  P₁, является оптимальным.

С помощью подобных замен в пределах множества оптимальных пла­нов можно добиться того, чтобы план, не теряя свойства оптимальности, приобрел некоторые дополнительные полезные свойства. Pазумеется, для этого необходимо, чтобы транспортная задача обладала не одним, а многими реше­ниями, что, конечно, на практике встречается далеко не всегда

Пользуясь изложенной задачей, можно находить оптимальные реше­ния распределения земляных масс при проектировании производства зем­ляных работ, выполняемых, например при возведении железнодорожного земляного полотна

Пусть заданный участок представлен продольным профилем с гра­фиком попикетных объемов (рис. 1).

Прежде всего нужно разбить продольный профиль на отдельные уча­стки ~ массивы, которые при решении задачи будут рассматриваться как поставщики (выемки) и потребители (насыпи). Желательно, каждую на­сыпь и каждую выемку, если они не очень протяженные (400...600 м), представить как массив, определив по графику попикетных объемов его объем. Если в пределах насыпи или выемки имеется несколько достаточно протяженных участков с примерно равными рабочими отметками, их вы­деляют как отдельные массивы. Однако делать это нужно очень осторожно, так как граница между массивами, как и в графике попикетных объемов, вертикальная, а технология механизированной разработки грунта подразу­мевает работу горизонтальными проходками. Учитывая местные условия и возможные ограничения, оговоренные в задании на проектирование, намечаются резервы, кавальеры, карьеры и отвалы.

При выполнении курсового проекта можно руководствоваться следующим:

-  объем резерва (кавальера) равен объему соответствующей насыпи (выемки), но не больше 6000 м³ на пикет;

-  объем намеченных карьеров можно принимать на порядок выше суммы объемов всех насыпей участка;

-  объем всех намеченных отвалов следует принимать таким, чтобы учитывалось известное ограничение:

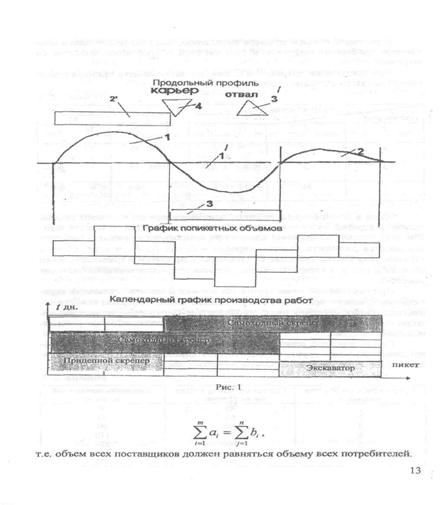
В рассматриваемом примере выделенные массивы поставщиков обозначены арабскими цифрами, а потребителей - арабскими цифрами со штрихом.

При построении матриц Р и С для рассматриваемого примера нужно воспользоваться данными табл. 2.2:

Таблица 2.2

Здесь в левой стороне таблицы приведены номера и объемы постав­щиков, в верхней части - номера и объемы потребителей. В правом верхнем углу каждой выделенной клетки при возможности реальной поставки указывается дальность транспортировки – lij (l₁₁ l₁₂ l₁₃ и т.д.); в левом верхнем углу клетки указывается стоимость разработки и транспортировки грунта Cij, внизу, в середине клетки, указывается объем поставки (если она имеется).

При продольной возке грунта (из выемки в насыпь) дальность перемещения lij можно принимать как расстояние между центрами тяжести соответствующих массивов плюс 50-70 метров. Центр тяжести массива на­ходят как центр тяжести площади графика попикетных объемов рассматриваемого массива.

При поперечной возке (из резерва в насыпь или из выемки в кавальер) дальность возки грунта зависит от расстояний между въездами и съез­дами. В курсовом проекте можно пользоваться данными табл. 2.3.