Проектирование производства земляных работ. Часть 1 (Распределение земляных масс. Способы разработки грунтов): Методические указания к курсовому и дипломному проектированию, страница 2

                    2.2.1. Организация и технология строительного процесса разработки выемки:

-                   - произвести окончательный выбор средств механизации;

-                   - описать, чем и как разрабатывается выемка;

-                   - запроектировать забой для выбранного экскаватора;

-                   - разбить выемку на проходки;

- показать на чертеже план и разрезы выемки, схемы погрузки автосамосвалов в двух-трех забоях;

-                   - определить потребное количество самосвалов на разных этапах разработки;

-                   - свести результаты в таблицу по прилагаемой форме:

2.2.2. Технико-экономические показатели

 3. ТЕХНОЛОГИЯ ПРОИЗВОДСТВА ПОДГОТОВИТЕЛЬНЫХ РАБОТ НА ЗАДАННОМ УЧАСТКЕ

              4.ТЕХНОЛОГИЯ ОТДЕЛОЧНЫХ РАБОТ НА УЧАСТКЕ ПК...ПК           

              5.КАЛЕНДАРНЫЙ ГРАФИК ПРОИЗВОДСТВА ЗЕМЛЯНЫХ РАБОТ НА -УЧАСТКЕ

Описать, как проектировался график, привести расчеты сроков производства работ. Дать описание окончательного варианта графика.

6. НАУЧНО-ИССЛЕДОВАТЕЛЬСКАЯ ЧАСТЬ

6.1. Технология закрепления грунтов ва пикетах ПК...ПК

6.2._____________________________________

2. РАСПРЕДЕЛЕНИЕ ЗЕМЛЯНЫХ МАСС

Одним из основных вопросов при проектировании производства земляных работ является вопрос о вывозе грунта из выемок и доставка его в насыпи. Решение этой задачи называют обычно распределением земляных масс. Поскольку способы разработки и транспортировки грунта во многом определяют стоимость строительства, его сроки, то одновременно с решением вопроса о распределении земляных масс решается и вопрос о способе производства работ, т.е. о выборе землеройных и транспортных машин.

Задача распределения земляных масс многовариантна, поэтому необ­ходимо найти наиболее выгодный, оптимальный вариант. Для решения згой задачи применена так называемая транспортная задача, или задача о назначениях, являющаяся частным случаем линейного программирования.

Название транспортной рассматриваемая задача [1] получила потому, что к ней сводится оптимизация плана перевозок грузов из т пунктов отправления с запасами а₁,..., а_т в п пунктов назначения с потребностями b₁,…b_n Роль коэффициентов с_ij в целевой функции играют удельные стоимости, т.е. стоимости перевозки одной единицы груза из пункта / в пункту. Задача состоит в минимизации общей стоимости, перевозки грузов при условии, что грузы оказываются полностью вывезенными из всех пунктов отправления и потребности всех пунктов назначения оказываются полностью удовлетворенными.

Переменные в этой задаче удобно снабжать индексами  i, j Если первый индекс принимает т значений, а второй - п, то общее число перемен­ных Ху (размерность задачи) равно, очевидно, тп. Сущность задачи состоит в минимизации целевой функции

при т + п ограничениях типа равенств:

Обычно предполагается дополнительное соблюдение равенства

иначе здача не будет иметь решений.

                При этих условиях имеется решение сформулированной задачи минимизации, содержащее не более т + п - 1 ненулевых значений перемен­ных Ху . Мы будем называть их назначениями.

При решении транспортной задачи пользуются двумя тп матрицами -матрицей планов Р =| p_t|_j и матрицей удельных стоимостей С =| c,j| , подвергая их специальным преобразованиям. Для формирования матри-цы Р на начальном шаге делается ровно т + п - 1, назначений (некоторые из них могут быть нулевыми) с тем, чтобы, во-первых, удовлетворялись условия

   (i=1,2,…m)

   (j=1,2,…n)

во-вторых, чтобы выбранные (для назначений) элементы матрицы не образовывали ни одного цикла. Под циклом здесь понимается последовательность элементов матрицы l₁, l₂,…l_k+1 (k > 1), начинающихся и кончающихся одним и тем же элементом (любые ее два соседних элемента распо­ложены либо в одном столбце, либо в одной строке). Пример такого цикла (l₁, l₂, l₃, l₄, l₅, l₆) дает матрица

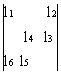
в которой явно выделены лишь элементы, образующие цикл. При этом элементы (l₁, l₃, l₅,) составляют так называемый нечетный полуцикл цикла (l₁, l₂, l₃, l₄, l₅, l₆) (с фиксированным началом цикла l₁), а элементы цикла l₂, l₄, l₆- четный полуцикл.

Удовлетворяющий этим условиям начальный выбор может быть сде­лан последовательным (по строкам., а внутри строки — по столбцам) при помощи максимальных назначений, лимитируемых лишь имеющимися за­пасами и потребностями (так называемый принцип северо-западного угла). Например, для a₁ = 10, a₂ = 15, а_з = 20; b₁ = 15 ,b₂= 15, b₃=10, b₄ = 5 на­чальные назначения приведены в табл. 2.1.

                                                                                                                                                    Таблица 2. 1

                                Строки этой таблицы озаглавлены запасами <я/ в пунктах отправления, а столбцы - потребностями bj в пунктах назначения. Первое назначение в первой строке исчерпывает весь запас в первом пункте отправления, второе назначение исчерпывает остающиеся потребности первого пункта назначения и т.д. Общее число назначений (равное 6) удовлетворяет условию m+n-1 (3+4-1=6), циклы отсутствуют, так что начальную матрицу планов

P =

можно считать построенной.

Пусть матрица удельных стоимостей имеет вид:

C =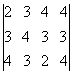

Жирным шрифтом в ней выделены элементы, соответствующие сделанным назначениям. Преобразования матрицы С состоят в прибавлении ко всем элементам одной и той же строки или одного и того же столбца не­которой константы (положительной или отрицательной). Целью таких пре­образований является обращение в нуль всех выделенных элементов мат­рицы (в случае, когда выделенные элементы матрицы не составляют цикла, достижение этой цели оказывается всегда возможным).