![]() 2.11
2.11
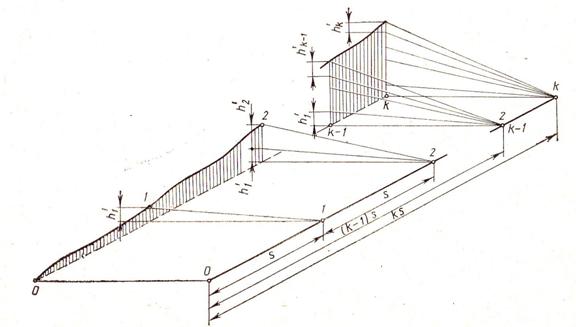
Рис. 2.8. Переход от перекосов на базе s к перекосам на базе ks
При непрерывном измерении перекоса способом, следующим из формулы (2.7), используется принцип: перекос равен разности двух возвышений. Однако этот принцип обладает определенными неудобствами, вытекающими из того, что перекос g3 — это угол γ (х) между двумя осями измерений, находящимися на расстоянии s. Наклон первой оси в точке х по отношению к горизонтали равен φ (х), а другой— в точке (х + s) — равен φ (х + s). Тогда перекос
γ (х) = φ (х) — φ (х + s) 2.12
Большинство средств измерения позволяют получать не абсолютные угловые значения, а лишь разность между φ (х) и φ (х + s). В случае периодических отступлений от нормы при базе измерения s, равной или кратной периодичности отступления λ, разность у (х)
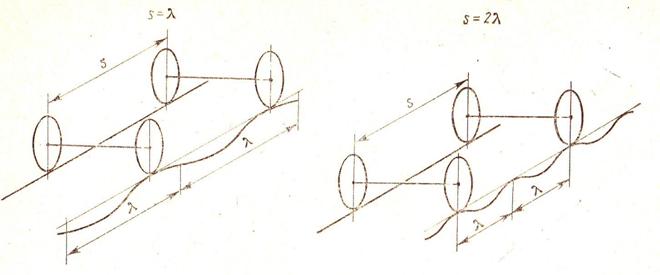
Рис. 2.9. Случаи, когда непрерывное измерение не выявляет фактических прямых и разносторонних перекосов пути
будет равна нулю (рис. 2.9). Частные случаи, показанные на рис. 2.9, встречаются очень редко. Отображение перекоса связано с определенной погрешностью, даже когда эти отступления не носят регулярного характера.
Роль измерения разносторонних перекосов пути длительное время недооценивалась. Появление в шестидесятых годах тяжелых вагонов с высокой поперечной жесткостью на скручивание (крупные цистерны, цементовозы и т. п.) привело к учащению случаев схода с рельсов. Многочисленные исследования показали, что причинами сходов чаще всего были: высокая жесткость вагонов на скручивание (сочетающаяся иногда с перекосом их конструкции), а также прямые и разносторонние перекосы пути. Поэтому уменьшение перекосов является одним из главных средств борьбы со сходами.
3.4.2. Измерения прямых и разносторонних перекосов
Измерение перекосов носит в буквальном смысле сплошной характер и выполняется преимущественно с помощью путеизмерительных вагонов. Реже применяют тележки.
2.5. ГОРИЗОНТАЛЬНЫЕ НЕРОВНОСТИ И ПОЛОЖЕНИЕ РЕЛЬСОВЫХ НИТЕЙ В ПЛАНЕ
2.5.1. Характеристики и величины
Любая неравномерность кривизны пути в кривой (см. рис. 2.1) приводит к изменению ускорения подвижного состава. Аналогично местная кривизна на прямых участках пути мешает нормальному движению поездов. И те, и другие горизонтальные неровности снижают плавность движения. При определенных значениях этих неровностей может наступить интенсивный рост деформаций. Чрезмерная деформация рельсовых нитей в плане может даже явиться причиной схода подвижного состава с рельсов.
Роль измерения горизонтальных неровностей в диагностике верхнего строения пути возросла еще больше с момента внедрения высоких скоростей движения поездов.
Определить относительные неровности, обозначенные на рис. 2.1 буквой у, очень трудно, в связи с чем обычным способом измерения является их соотнесение с жесткой базой l. Измеряя расстояние от точек, определенных на этой базе, до рельсовой нити, получают отметки f (рис. 2.11), которые являются стрелами изгиба кривой (для других точек так и будем их называть, учитывая условность этого определения).
Способ измерения стрелы, показанный на рис. 2.13 (со смещением места измерения на половину базы), — не единственный. На железных дорогах Германии применяют измерение стрел на хорде 16 м, при этом место измерения всегда смещают на 174 хорды, т. е. на 4 м (рис. 2.14).
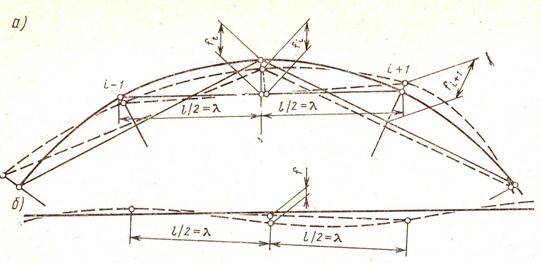
а — в кривых от хорды длиной l; б — в деформированном пути на прямом участке
Рис. 2.13. Измерение горизонтальных неровностей стрел
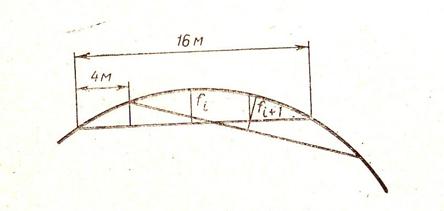
Рис. 2.14. Принцип измерения стрел на желез-
и ных дорогах Германии
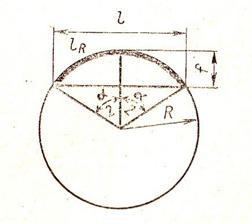
Рис. 2.15. Длина пути lR и хорды l
Измерение стрелы на хорде lсвободно от какой-либо существенной ошибки, если эту длину откладывают непосредственно на рельсе. Для иллюстрации ничтожности ошибки вычислим разность между длиной дуги 1% и длиной лежащей на ней хорды l (рис. 2.15). Из простых геометрических зависимостей следует:
![]()
и
![]()
откуда
![]() 2.13
2.13
Принимая R = 180 м и lR =20 м, после подстановки получим
![]()
Стрела, вычисленная для этой хорды по обычно применяемой'' формуле
![]() 2.14
2.14
равна 277,49 мм, тогда как для хорды 20,000 м она равна 277,77 мм. Следовательно, ошибка равна 0,28 мм, т. е. гораздо меньше точности самого измерения,, равной при такой хорде 1 мм. Для больших радиусов кривой эта разность еще более уменьшается.
Ошибку такого же порядка дает применение приближенной формулы (2.14). Для R — 180м и I = 20 м стрела согласно точной формуле
![]() 2.15
2.15
равна 277,99 мм. Анализируя эти ошибки, можно убедиться, что предлагаемые упрощения расчетов и измерений не сказываются отрицательно на конечных результатах.
Рекомендуется подбирать длину хорды / в соответствии с радиусом кривой R, чтобы относительная точность измерения была постоянной:
R, м <650 650—2650 >2650
l, м ' 10 20 30
3.5.2. Измерение горизонтальных неровностей
Классификация методов измерения показана на рис. 2.17. В диагностике верхнего строения пути применяются относительные измерения стрел или углов набегания скользунов путеизмерительного вагона.
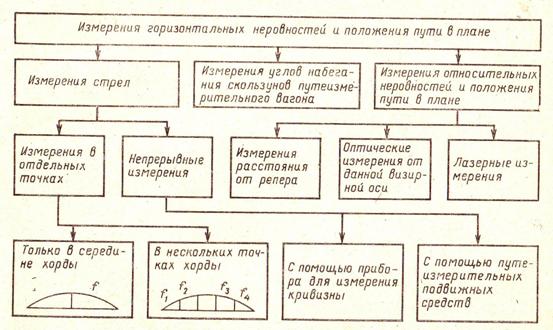
Рис 2.17 Классификация методов измерения горизонтальных неровностей
Величину стрел в отдельных точках наиболее часто измеряют в ручную, а также стреломерами, состоящими из двух держателей, накладываемых на головку рельса, и линейки. На линейке и держателях имеются уровни, облегчающие их установку в положение, при котором точки крепления нейлоновой нити или проволоки (0,3—0,5 мм) находятся на равном расстоянии от боковой поверхности рельса.
Ручные стреломеры позволяют легко, быстро и точно измерять стрелу изгиба кривой. При надлежащем натяжении проволоки и умеренном ветре точность измерения достигает 1 мм.
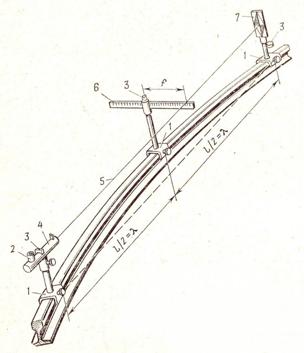
1-Зажим; 2-окуляр; 3-уровень; 4-визирная труба; 5-ось мишени; 6-горизонтальная рейка; 7-указатель мишени
Рис 2.18 Устройство оптического стреломера
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.