АПШ-2 устанавливается на точку измерения
и нажимается кнопка ИЗМерение. Схема получает питание от БП, запускается
программа из ПЗУ, начинается процесс измерения. Сигналы с датчиков ширины и
уровня колеи в блоке АЦП нормализуются и представляются в цифровом виде. ЦП их
обрабатывает и выводит на индикацию. Первым индицируются значение базового
размера колеи ("шаблон") в миллиметрах, а потом превышение или
понижение относительно рихтовочной нити ("уровень"), также в
миллиметрах со знаком.
При включении тумблера ЗАПись данные замера вместе с данными привязки,
предварительно набранными на ПУ, записываются в ОЗУ и там хранятся. После
записи система автоматически отключает питание схемы, за исключением ОЗУ. ОЗУ
переходит в режим малого потребления, при этом записанные данные сохраняются.
Такое включение и выключение питания реализовано с целью экономии ресурса
аккумулятора. Данные замера, накопленные в ОЗУ, можно вызвать на индикацию
Рис 2.5 АПШ в работе
2.3. ПОЛОЖЕНИЕ РЕЛЬСОВЫХ НИТЕЙ ПО УРОВНЮ. ВОЗВЫШЕНИЕ ОДНОГО РЕЛЬСА НАД ДРУГИМ
2.3.1. Характеристики и величины
Положение рельсовых нитей по уровню в сечении пути (рис. 2.6) после ширины колен — наиболее часто измеряемая величина. На прямом участке обе рельсовые нити должны быть в одном уровне, за исключением таких особых случаев, как возвышение, выполненное на короткой прямой вставке между кривыми, или отвод возвышения. Возвышением называют разность высот рельсовых нитей.
Широкое применение измерений положения рельсовых нитей по уровню обусловлено его простотой. Результаты измерения, как и в любом другом случае, сравнивают с допускаемыми отклонениями. Условность принятия допускаемых отклонений для положения рельсовых нитей по уровню намного выше, чем для остальных измеряемых величин. Само по себе отклонение положения по уровню не оказывает большого влияния на степень динамического воздействия подвижного состава на верхнее строение пути, а поэтому редко в отличие, например, от прямых и разносторонних перекосов может вызвать состояние неработоспособности. Равномерное отклонение положения рельсовых нитей по уровню на прямых участках встречаются реже, чем перекосы. Согласно исследованиям отношение длины пути с равномерным отклонением положения по уровню к длине пути с перекосами равно 0,5. Несмотря на это, изучение положения рельсовых нитей по уровню имеет большое значение для диагностики верхнего строения пути, поскольку анализ соответствующих результатов позволяет определить перекосы и представить себе картину качества выполненных работ.
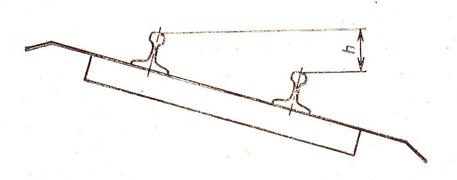
Рис. 2.6. Возвышение рельсовых нитей в кривой
2.3.2. Средства измерения положения рельсовых нитей по уровню
Возвышения в прямых и кривых измеряют так же часто, как и ширину колеи. Обычно для этой цели применяют те же средства измерения: универсальные ручные путевые шаблоны, самопишущие шаблоны или реже путевые уровни. Возвышения измеряют в тех же сечениях, что и ширину колеи. Числа, характеризующие возвышение, являются алгебраическими. Рекомендуется применять единую запись знака минус (например, при результате, означающем понижение правой нити, если смотреть в направлении увеличения километража).
Различать положительные и отрицательные возвышения рельсовых нитей необходимо с точки зрения определения прямых и разносторонних перекосов.
2.3.3. Изменение положения рельсовых нитей по уровню
Изменение положения рельсовых нитей по уровню по существу непрерывно нарастает по мере увеличения общей наработки. Этот рост зависит от конструкции верхнего строения пути, качества его содержания (в том числе и качества работ), нижнего строения пути и от характера нагрузки. Однако дать обобщенное описание этих изменений не представляется возможным.
2.4 ПРЯМЫЕ И РАЗНОСТОРОННИЕ ПЕРЕКОСЫ
2.4.1. Характеристики и величины
Рассмотрим участок пути длиной s (рис. 2.7), на котором рельсовые нити имеют определенные отклонения от теоретической плоскости, обозначенной точками 1L, 1P, 2P и дополнительно 2L. Отклонения нитей в этих точках соответственно равны zll, z1p, z2p, z2l.
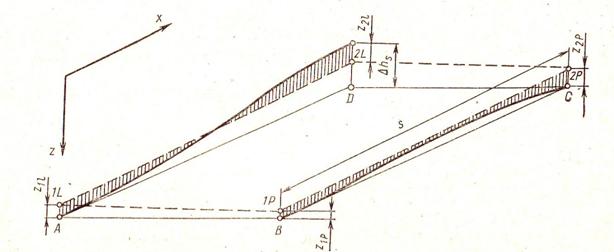
Рис. 2.7. Принцип измерения прямых и разносторонних перекосов пути
Если рельсовая нить находится ниже теоретической плоскости, ее отклонение будем считать положительным.
Разница по уровню рельсовых нитей на длине s:
Их разность отнесенная к сечению 2:
2.7
Для удобства запоминания выражение (2.17) можно написать иначе:
2.7а
Отклонение по уровню обеих рельсовых нитей
Исходя из способа измерения прямые и разносторонние перекосы пути проверяют на участке s порядка нескольких метров. Следовательно, имеем
2.
8
Разность 
которую в соответствии с выражением (2.7) вычисляют как
разность сумм деформаций рельсовых нитей на двух диагоналях, представляет
собой расстояние между одной из четырех точек и плоскостью, определяемой
остальными тремя точками, лежащими на деформированных рельсовых нитях в обоих
сечениях измерения (в рассматриваемом случае точками А, В, С).
Этот принцип с точностью, достаточной для практических целей, можно применить и к нитям в кривых с возвышением, где теоретическая плоскость заменяется конической поверхностью.
Из рис. 2.7. следует, что наиболее часто применяемый метод пересчета перекоса g1 с базой s1 на перекос g2 с базой s2 по формуле
может быть связан с большой ошибкой, особенно при малых протяжениях неровностей и значительной амплитуде.
Более точный метод пересчета перекоса применим для перехода от базы s к базе ks, где k — целое число.
С этой целью следует рассмотреть случай относительной неровности, показанный на рис. 2.8. Перекос, измеренный на базе s в сечении 1—1:
2.9
где h1— относительная неровность пути в сечении /—/. Перекос на той же базе, но в сечении 2—2
2.
9а
В то же время перекос на базе 2s в сечении 2—2 определяется зависимостью
2.10
Итак, в общем виде для перекоса на базе ks в сечении k имеем
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.