Государственное образовательное учреждение
высшего профессионального образования
Петербургский государственный университет путей сообщения
(ПГУПС)
Кафедра: «Железнодорожный путь».
Дисциплина: «Железнодорожный путь».
Курсовой проект на тему: «Железнодорожное земляное полотно».
Выполнил:
студент гр. СЖУ-103
Стельмах А Н
Принял:
Романов А В
Санкт-Петербург
2005г.
1 РАЗДЕЛ.
Расчёт железнодорожного пути на прочность.
Основные характеристики пути и подвижного состава сводятся в таблицу №1.
Таблица №1.
|
Наименование характеристики |
Единицы измерения |
Величина. |
|
|
Локомотив |
Вагон |
||
|
1. Статическая
нагрузка от колеса на рельс - |
кН |
110,4 |
120 |
|
2.Расстояние между осями в тележке- |
м |
|
|
|
3. Неподрессоренный
вес, отнесённый к одному колесу- |
кН |
41,8 |
9,95 |
|
4. Жёсткость
комплекта рессор- |
МН/м |
1,3 |
2,00 |
|
5. Диаметр колеса по среднему кругу катания - d |
м |
1,05 |
0,95 |
|
6. Скорость движения - V |
м/с |
22,2 |
22,2 |
|
7. Коэффициент
перехода от осевых напряжений к кромочным - f |
- |
Прямые – 1,20 Кривые – 1,46 |
Прямые – 1,18 Кривые – 1,33 |
Расчётные характеристики пути сводятся в таблицу №2.
Таблица №2
|
Наименование характеристики |
Единицы измерения |
Величина. |
|
|
Прямая |
Кривая R=750м |
||
|
1. Тип рельса/ приведённый износ |
-/мм |
Р65/6 |
Р65/6 |
|
2.Материал шпал |
Железобетон |
||
|
3. Эпюра/ расстояния между осями шпал - е |
-/м |
1840/0,55 |
2000/0,50 |
|
4. Толщина балласта под шпалой |
м |
0,50 |
|
|
5. Модуль упругости подрельсового основания - u |
МПа |
Лето – 150 Зима - 170 |
Лето – 167 Зима - 185 |
|
6. Момент инерции
рельса в вертикальной плоскости относительно горизонтальной оси- |
|
|
|
|
7. Момент
сопротивления рельса относительно наиболее удалённого волокна на подошве - |
|
|
|
|
8. Коэффициент соотносительной жёсткости подрельсового основания и рельса - k |
|
Лето – Зима - |
Лето – Зима - |
|
9. Коэффициенты к расчёту дополнительной динамической силы инерции, возникающей при прохождении колесом неровности на пути
|
|
|
|
|
10. Площадь рельсовой подкладки - |
|
|
|
|
11. Площадь
полушпалы с поправкой на изгиб - |
|
|
|
|
12. Коэффициенты к расчёту напряжений на основной площадке земляного полотна
|
|
|
|
1.2.Определение динамического воздействия от колеса на рельс.
1.2.1. Среднее значение динамической силы воздействия от колеса на рельс.
![]() , где
, где
![]() -
статическое воздействие колеса на рельс, кН;
-
статическое воздействие колеса на рельс, кН;
![]() - среднее значение дополнительной
динамической силы
инерции,
возникающей
при колебании кузова на рессорах, кН.
- среднее значение дополнительной
динамической силы
инерции,
возникающей
при колебании кузова на рессорах, кН.
![]() =
= ![]()
![]() - максимальное динамическое
воздействие, возникающее при колебаниях кузова на рессорах, кН.
- максимальное динамическое
воздействие, возникающее при колебаниях кузова на рессорах, кН.
![]() , где
, где
![]() жёсткость комплекта рессор, МН/м;
жёсткость комплекта рессор, МН/м;
![]() - максимальный прогиб рессор;
- максимальный прогиб рессор; ![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
Расчёты:
Для локомотива
![]() =
= ![]()
![]() =
=
![]()
![]() =
= ![]()
![]() =
=
![]()
![]()
Для вагонов
![]() =
= ![]() =
=
![]()
![]() =
= ![]()
![]() =
= ![]() =
=
![]()
![]() =
= ![]()
1.2.2. Максимальное вероятное динамическое воздействие от колеса на рельс.
![]() , где
, где
![]() - среднеквадратическое отклонение от
средней динамической силы.
- среднеквадратическое отклонение от
средней динамической силы.
![]() =
= ![]() ,
где
,
где
![]() -среднеквадратическое отклонение от
силы инерции, возникающей при колебании кузова на рессорах;
-среднеквадратическое отклонение от
силы инерции, возникающей при колебании кузова на рессорах;
![]() - среднеквадратическое отклонение от
силы инерции, возникающей при прохождении неровности на пути;
- среднеквадратическое отклонение от
силы инерции, возникающей при прохождении неровности на пути;
![]() -среднеквадратическое отклонение от
силы инерции, возникающей при прохождении непрерывной неровности на колесе;
-среднеквадратическое отклонение от
силы инерции, возникающей при прохождении непрерывной неровности на колесе;
![]() -среднеквадратическое отклонение от
силы инерции, возникающей при прохождении изолированной неровности на колесе.
-среднеквадратическое отклонение от
силы инерции, возникающей при прохождении изолированной неровности на колесе.
![]() =
= ![]()
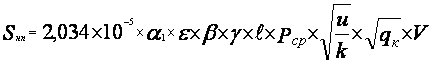
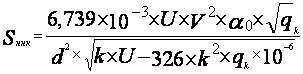 , где
, где
![]() - коэффициент, характеризующий
отношение необрессоренной массы колеса и участвующий во взаимодействии массы
пути,
- коэффициент, характеризующий
отношение необрессоренной массы колеса и участвующий во взаимодействии массы
пути, ![]() = 0,403
= 0,403
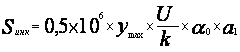 , где
, где
![]() - максимальный дополнительный прогиб
рельса, возникающий при прохождении колесом неровности на пути, отнесённый к
глубине неровности,
- максимальный дополнительный прогиб
рельса, возникающий при прохождении колесом неровности на пути, отнесённый к
глубине неровности, ![]() =1,47
=1,47
![]() - расчётная глубина изолированной
неровности на колесе, м; принимается
- расчётная глубина изолированной
неровности на колесе, м; принимается ![]() =
=![]() ;
;
![]() - предельно допустимая глубина
ползуна на колёсах по ПТЭ, м;
- предельно допустимая глубина
ползуна на колёсах по ПТЭ, м;
![]() ,
,
![]()
Пример расчётов:
Для локомотива
![]() =
= ![]() =
= ![]()
-в прямом участке
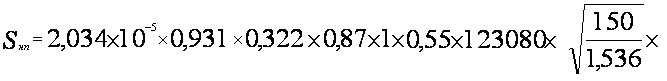
![]() =
=![]()
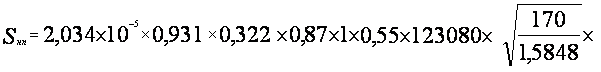
![]() =
=![]()
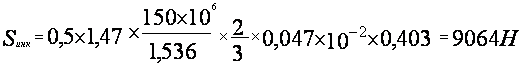
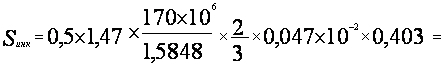
![]()
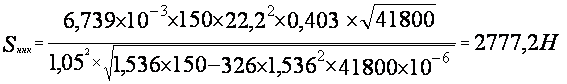
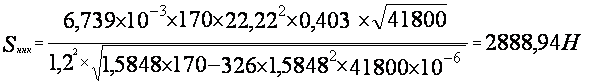
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]() =
= ![]()
-в кривой
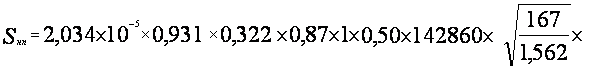
![]() =
=![]()
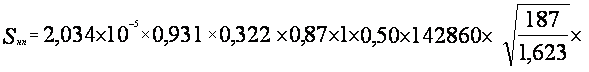
![]() =
=![]()
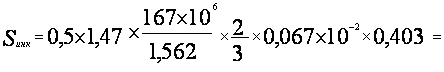
![]()
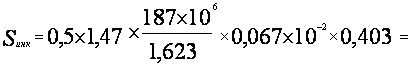
![]()
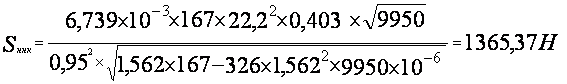
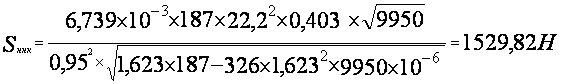
![]() =
= ![]()
![]() =
= ![]()
Результаты расчётов сводятся в таблицу №3.
Определение максимального динамического воздействия от колеса на рельс.
Таблица №3
|
Условие |
|
|
|
|
|
|
|
|
||
|
Локомотив |
Пря мая |
Л |
12680 |
123080 |
1352 |
16108 |
9064 |
2777 |
16515 |
164366 |
|
З |
16882 |
9956 |
2889 |
17312 |
166361 |
|||||
|
Кри вая |
Л |
15322 |
9923 |
2885 |
15793 |
162563 |
||||
|
З |
15906 |
10694 |
2979 |
16401 |
164081 |
|||||
|
Вагон |
Пря мая |
Л |
22860 |
142860 |
2438 |
9121 |
12920 |
1412 |
9969 |
167783 |
|
З |
9560 |
14192 |
1478 |
10381 |
168812 |
|||||
|
Кри вая |
Л |
8676 |
14145 |
1365 |
9643 |
166969 |
||||
|
З |
9007 |
15244 |
1530 |
10046 |
167974 |
|||||
1.3. Определение напряжений в элементах верхнего строения пути.
При определении ![]() расчетная ось всегда первая, т.к.
расчетная ось всегда первая, т.к. ![]() для любых типов подвижного состава.
для любых типов подвижного состава.
При определении ![]() если
если ![]() ,
то расчетная ось первая, если
,
то расчетная ось первая, если ![]() , то расчетная ось
вторая.
, то расчетная ось
вторая.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.