Решенные задачи к экзамену по общественному здоровью и здравоохранению

№ 1

Параметрические методы оценки достоверности статистического исследования. Метод стандартизации. Корреляционный анализ, 2008

1. При изучении средней длительности лечения больных в хирургическом и терапевтическом отделениях городской больницы были получены следующие данные: средняя длительность лечения в хирургическом отделении составила 12,1 (m1= ± 0,05) дней, а в терапевтическом ― 23,2 (m2 = ± 0,09) дней. Общее число лечившихся составило ― 405 человек.

Определить достоверность разности средней длительности лечения в сравниваемых группах.

Дано: средняя длительность лечения (средняя величина интенсивного показателя Р):

            Р_{1 =} 12,1 (дней) (средняя длительность лечения в хирургическом отделении),

            m_{р1 =} ± 0,05 (дней) (средняя ошибка средней величины интенсивного показателя Р₁);

            Р_{2 =} 23,2 (дней) (средняя длительность лечения в терапевтическом отделении),

            m_{р2 =} ± 0,09 (дней) (средняя ошибка средней величины интенсивного показателя Р₂);

            n = 405 (человек) (число наблюдений), причем n˃30.

Найти: достоверность разности средней длительности лечения в сравниваемых группах (сравнить два однородных интенсивных показателя достоверности Р_{1 и} Р_2)..

Решение: При необходимости сравнения двух однородных показателей достоверность их различий определяется по формуле:

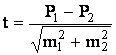, где P₁–P₂ (от большего числа отнимают меньшее) ― разность двух сравниваемых показателей,  ― средняя ошибка разности двух показателей.

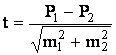 = , причем t˃2 и даже t˃3

 (т. е. на 99,7 – 99,9 %), (при n˃30 разность двух однородных интенсивных показателя достоверности Р_{1 и} Р₂ статистически достоверна, если t = 2 или больше, т. е. ˃95,5 %).

       Ответ: средняя длительность лечения в терапевтическом отделении больше чем в хирургическом отделении, что статистически достоверно на 99,7 – 99,9 %.

2. Определить корреляционную связь между возрастом и числом госпитализированных больных с сердечной недостаточностью.

Возраст в годах (Х)	Число госпитализированных (У)
До 20 лет	12
20–29	24
30–39	30
40–49	23
50–59	26
60 и старше	30

3. Дать сравнительный анализ деятельности по городским больницам №1 и №2, применив  прямой метод стандартизации.

За стандарт принять число лечившихся в больнице № 1.

Отделение	Больница № 1			Больница № 2			«Ожидаемо число» умерших
	Число лечив. (СТАНДАРТ)	Число умерших	Летальность (интенсивный показатель)	Число лечив.	Число умерших	Летальность (интенсивный показатель)	Больница № 1	Больница № 2
Терапевтическое	800	20	2,5	650	13	2,0	20	16
Хирургическое	700	11	1,6	450	5	1,1	11	7,7
Туберкулезное	500	30	6,0	900	45	5,0	30	25
Всего	2000	61	3,1	2000	63	3,2	61	64

Решение осуществляется прямым методом стандартизации в несколько этапов:

I этап – вычисление интенсивных показателей.

В нашем случае  – нахождение числа умерших на 100 больных (т.е. летальность) в каждой больнице и в каждом отделении.

Например, для больницы 1:

На 800 больных приходиться 20 умерших,

На 100 больных приходиться х умерших, х = 20*100/800 = 2,5.

В данной задаче летальность дана в условии.

II этап – выбор стандарта. За стандарт обычно берут распределение по устраняемому фактору одной из сред, либо их сумму, либо подсумму. Однако, стандарт можно выбрать любой, по нашему смотрению.

В данной задаче стандарт  дан в условии - за стандарт принять структуру  лечившихся в больнице 1.

III этап – вычисление ожидаемых чисел.              Необходимо вычислить, какова была бы величина сравниваемого явления, если бы частные интенсивные показатели остались прежними, а распределение среды было бы таким, как по стандарту.

Больница 1 (дано по условию, т.к. за стандарт принята структура лечившихся в больнице 1) - переписать значения столбца «Число умерших»:

На 100 лечившихся приходиться 2, 5 умерших,

На 800 лечившихся приходиться 20 умерших.

Больница 2:

На 100 лечившихся приходиться 2  умерших,

На 800 лечившихся приходиться х умерших, х=16;

На 100 лечившихся приходиться 1,1 умерших,

На 700 лечившихся приходиться х умерших; х=7,7;

На 100 лечившихся приходиться 5 умерших,

На 500 лечившихся приходиться х умерших, х=25;

На 100 лечившихся приходиться 3,2 умерших,

На 2000 лечившихся приходиться х умерших, х=64.

IV этап – вычисление стандартизованных показателей и их сравнение. Стандартизованные показатели рассчитываются, как и обычные интенсивные показатели, на величину стандарта.

Больница 1:

На 2000 больных приходиться 61 умерших,

На 100 больных приходиться х умерших, х=3,05.

Больница 2:

На 2000 больных приходиться 64 умерших,

На 100 больных приходиться х умерших, х=3,2.

Вывод: если бы количество лечившихся в больнице 1 и больнице 2 было бы одинаковым, то число умерших на 100 лечившихся (летальность) была бы выше в больнице 2 в сравнении с больницей 1.

4. Дать сравнительный анализ деятельности по двум городским больницам А и Б, применив метод стандартизации.

За стандарт принять структуру  лечившихся в больнице А.

Назв.болезни	Больница А			Больница Б			«Ожидаемо число» умерших
	Число больных (СТАНДАРТ)	Число умерших	Летальность % (интенсивный показатель)	Число больн.	Число умерших	Летальность % (интенсивный показатель)	Больница А	Больница Б
Гипертонич.б-нь.	180	4	2,2	200	4	2,0	4	3,6
Рак желудка	100	30	30,0	90	27	30,0	30	30
Инфаркт миокарда	120	8	6,7	160	10	6,3	8	7,6
Всего	400	42	10,5	450	41	9,1	42	36,4

Решение осуществляется прямым методом стандартизации в несколько этапов:

I этап – вычисление интенсивных показателей.

В нашем случае  – нахождение числа умерших на 100 больных (т.е. летальность) в каждой больнице и в результате различных болезней.

Например, для больницы А:

На 180 больных приходиться 4 умерших,

На 100 больных приходиться х умерших, х = 4*100/180 = 2,2.

В данной задаче летальность дана в условии.

II этап – выбор стандарта. За стандарт обычно берут распределение по устраняемому фактору одной из сред, либо их сумму, либо подсумму. Однако, стандарт можно выбрать любой, по нашему смотрению.