9.1 Реализация регулятора скорости в цифровой форме
соответствует замене передаточной функции W(p) в аналоговой системе передаточной функцией W(z), с
помощью применения стандартного z-преобразования: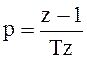 
, где Т-период
прерывания.
9.2 Применим метод прямоугольников, т.е.
,
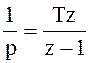(9.1)
Аналоговый прототип регулятора скорости, полученный
методом ЛАЧХ имеет вид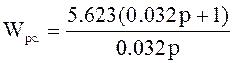 
.
Произведем замену соответственно выражению (9.1). Для начала представим
аналоговый прототип в виде
,
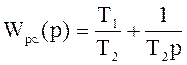(9.2)
Получим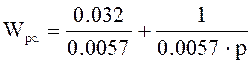 
,
и произведем замену (9.1):
,
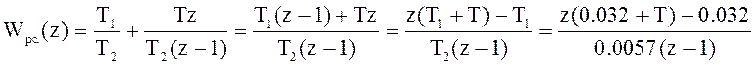(9.3)
9.3 Теперь проделаем то же, но используя более точное билинейное преобразование:
,
(9.4)
Получим:
,
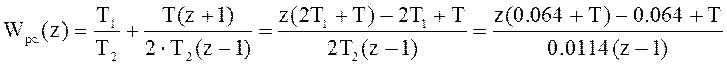(9.5)
9.4 Предлагается для каждого варианта аппроксимации определить алгоритм работы регулятора для двух значений периода прерывания
1 Т=0,5 min (Ta, Tm);
2 Т=5 min (Ta, Tm).
Т.к. Тм>Ta, то расчет произведем Т = 0,5Ta = 0.026 с и Т = 5Ta = 0.255 с.
9.5 Определим алгоритм работы цифрового регулятора, разделив полином числителя и полином знаменателя на наивысшую степень (т.е. на z), получим:
,
или из 
, получаем 
, (9.6)
Для билинейного преобразования выражение (9.6) приобретет вид:
,
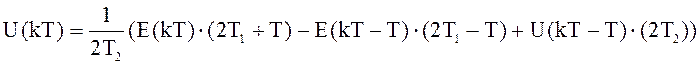(9.7)
10 АНАЛИЗ САУ С ЦИФРОВЫМ РЕГУЛЯТОРОМ
|
|
10.1 Для случая Т = 0,5Та = 0,0255 с, определим запасы устойчивости, для регулятора полученного стандартным z-преобразованием, пользуясь MATLAB 6.1 (Simulink).
|
|
Рисунок 10.1 ЛАЧХ и ЛФЧХ разомкнутой системы
Как видно из рисунков (10.1), процессы в САУ вышли в неустойчивость, следовательно, проводить дальнейшие исследования не имеет смысла, так как реакция на любой вид сигнала, на наброс нагрузки, на помеху даст расходящийся процесс. Это объясняется большим тактом квантования (0,0255 с), а в промышленных электроприводах для контура скорости период прерывания не может превышать (8 ¸ 10) Тm. Постоянная времени тиристорного преобразователя разрабатываемой системы была принята 0,002 с.
Увеличение периода прерывания приведет к еще большему снижению запасов устойчивости САУ, поэтому анализировать систему с периодом квантования 5Та, также нет смысла (полученные процессы будут расходящимися). Из вышесказанного следует, что для нормализации работы САУ необходимо уменьшить период прерывания до Т = 0,1Та = 0,0051 с.
10.2 Построим ЛАЧХ и ЛФЧХ для случая Т = 0,1Та = 0,0051 с, определим запасы устойчивости, для регулятора полученного стандартным z-преобразованием:
|
|
|
|
Рисунок 10.2 ЛАЧХ и ЛФЧХ разомкнутой системы
Как видно из рисунков (10.2), системы стала устойчивой
и имеет следующие запасы устойчивости: 
рад, 
дБ, полученные запасы ниже требуемых (
рад, 
дБ), но их можно считать удовлетворительными.
10.3 Смоделировав схему подадим на вход единичный ступенчатый сигнал
Рисунок 10.3 Временная диаграмма изменения скорости и тока
Сигнал был подан через апериодический фильтр, для
уменьшения перерегулирования, с единичным коэффициентом передачи и постоянной
времени Тф = 0,03 с. Фильтр позволил добиться практически нулевого
перерегулирования (по графику w(t): 
), при требуемом быстродействии (tр = 0,067 с).
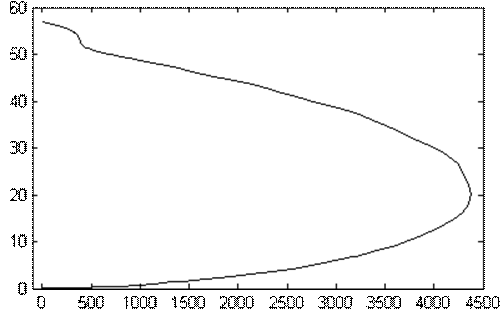
Рисунок 10.4 Динамическая электромеханическая характеристика
10.4 Представим реакцию САУ на ступенчатое приложение
нагрузки 
Рисунок 10.5 Временная диаграмма изменения скорости и тока при работе двигателя на заданную нагрузку
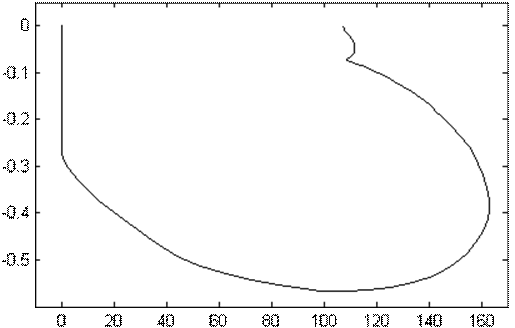
Рисунок 10.6 Динамическая электромеханическая характеристика
10.5 По графикам w(t) и i(t) определим установившуюся ошибку, вызванную
действием возмущения . Как
говорилось выше система обладает астатизмом первого порядка по отношению к
нагрузке, при набросе тока система отрабатывает без ошибки (Dw = 0),
т.е. 
, что видно из
графиков w(t) и w(i).
10.6 Представим результаты работы САУ при подаче на вход помехи
|
Рисунок 10.7 Вид заданной помехи
Рисунок 10.8 Временная диаграмма изменения скорости и тока при действии помехи
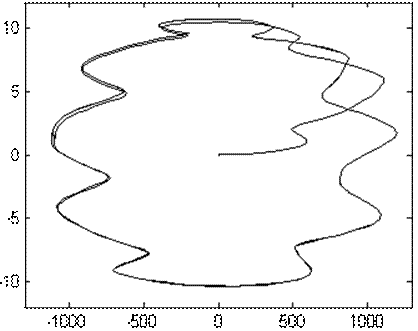
Рисунок 10.9 Динамическая электромеханическая характеристика
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
