Структурная схема заданной части САУ. Структурная схема двигателя постоянного тока с независимым возбуждением, страница 4

Рисунок 5.4 Динамическая электромеханическая характеристика

5.6 Представим реакцию САУ на ступенчатое приложение нагрузки , относительное значение нагрузки на валу I_c/I_н = 0,65, что соответствует I_с =107.25

Рисунок 5.5 График изменения угловой скорости во времени w(t)

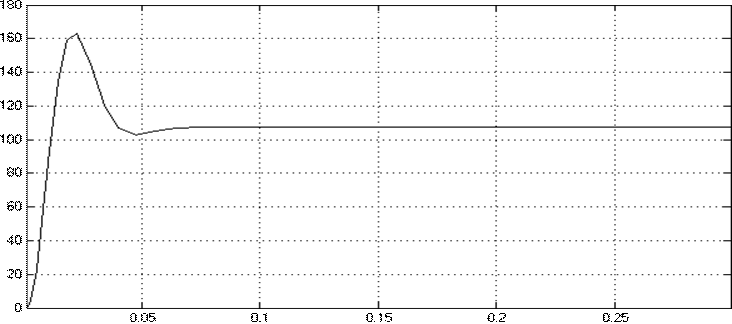
Рисунок 5.6 График изменения тока двигателя во времени i(t)

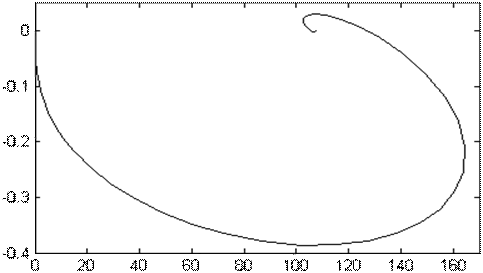
Рисунок 5.7 Динамическая электромеханическая характеристика

5.7 По графикам w(t) и i(t) определим установившуюся ошибку, вызванную действием возмущения . Как говорилось выше система обладает астатизмом первого порядка по отношению к нагрузке, при подаче ступенчатого сигнала по току система отрабатывает без ошибки (Dw = 0), т.е. , что видно из графиков w(t) и w(i).

5.8 Представим результаты работы САУ при подаче на вход помехи

Рисунок 5.8 График изменения угловой скорости во времени w(t)

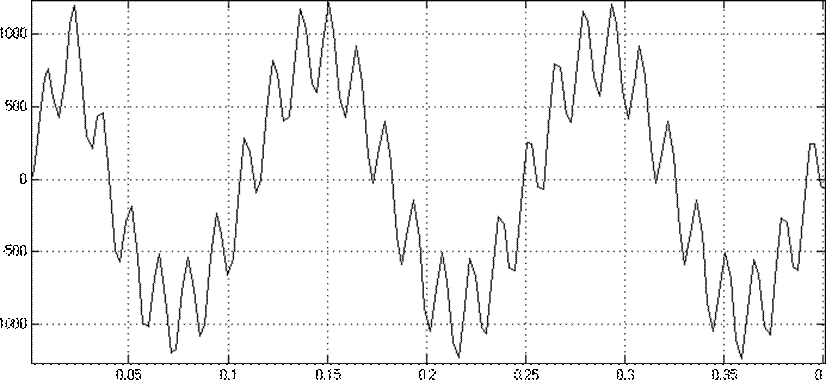
Рисунок 5.9 График изменения тока двигателя во времени i(t)

Рисунок 5.10 Динамическая электромеханическая характеристика

5.9 Определим коэффициент передачи САУ на основной гармонике

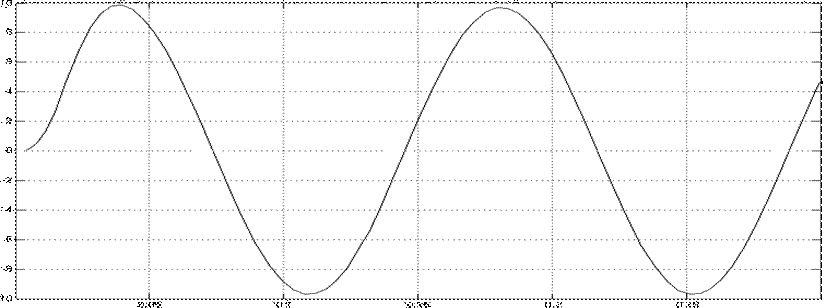
Рисунок 5.11 Реакция на основную гармонику

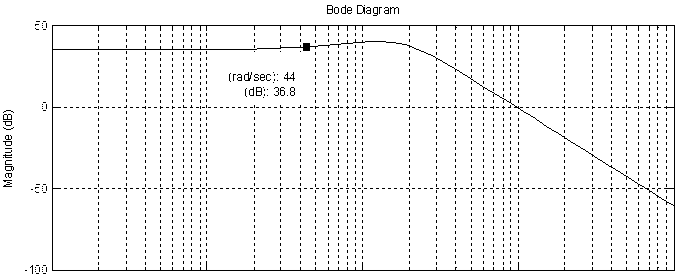
Рисунок 5.12 ЛАЧХ замкнутой системы

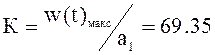При частоте основной гармоники 44 рад/сек: L(w)=20 Log (K) = 36,8 дБ, следовательно . Определим по реакции САУ на основную гармонику w(t)_макс = 9,71, при заданной а₁ = 0.14, следовательно , определенные коэффициенты совпадают с некоторой погрешностью.

6 СИНТЕЗ РЕГУЛЯТОРА СКОРОСТИ

МЕТОДОМ ЛАЧХ

6.1 Полученный регулятор скорости в результате синтеза должен удовлетворять всем требованиям, предъявляемым к системе. При синтезе полагаем, что все внутренние контуры САУ синтезированы в соответствии со стандартной методикой синтеза подчиненного регулирования, и кроме того, учитывать все связи в системе. Т.е. имея двухконтурную систему регулирования из ранее приведенных расчетов передаточная характеристика ПИ-регулятора тока соответствует выражению (4.2):

,

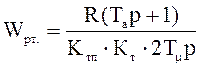В итоге получили ПИ-регулятор тока.

6.2 Структурная схема для синтеза, тогда будет выглядеть следующим образом

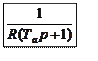
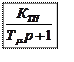
Рисунок 6.1

6.3 Построим ЛАЧХ данной системы

Рисунок 6.2 ЛАЧХ

6.4 Сформируем желаемую ЛАЧХ, исходя из требований:

1  Частота среза соответствует ;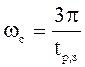

2  В окрестности частоты среза формируется желаемая часть ЛАЧХ (наклон -1, минимальная протяженность 1 декада, симметричность относительно частоты среза);

3  Низкочастотная асимптота имеет наклон -2 (т.к. нужно обеспечить астатизм 2-го порядка);

4  Наклон высокочастотной асимптоты желаемой характеристики совпадает с наклоном исходной, и в области высоких частот должна лежать не выше исходной.

Используя алгоритм, построим в одних осях желаемую и исходную характеристику, и вычитанием найдем ЛАЧХ желаемой характеристики

Рисунок 6.3 Нахождение ЛАЧХ корректирующего устройства

6.5 Очевидно, что корректирующее устройство представляет собой последовательное соединение интегратора и форсирующего звена 1-го порядка.

6.6 Полученную ЛАЧХ корректирующего устройства следует упростить, для этого аппроксимируем её. Несовпадение высокочастотных областей приведет к усилению высокочастотных помех, что является минусом системы, для ограничения помех принимают специальные меры, но в рамки курсового проекта это не входит.

Рисунок 6.4 Получение реализуемой желаемой ЛАЧХ

6.7 Определим параметры интегрирующего и форсирующего звена, чтобы получить передаточную функцию корректирующего устройства, пользуясь формулой

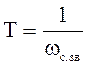,                                                   (6.1)

Интегратор: 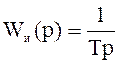, где  с

Форсирующее звено первого порядка: , где К=5.623 (найдено из 20Log(К)=15),  с.

Следовательно: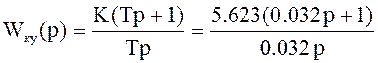

7 АНАЛИЗ СИНТЕЗИРОВАННОЙ САУ

7.1 Размыкаем систему и находим передаточную функцию разомкнутой системы.