При этом по схеме 4.3: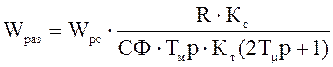 
, следовательно,
получим
,
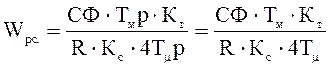(4.6)
В итоге получили П-регулятор скорости.
4.9 Найдем по схеме 4.3 (без учета усечения) передаточную функцию замкнутого контура скорости в целом, получим
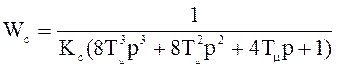, (4.7)
4.10 По заданию требуется обеспечить астатизм второго
порядка относительно сигнала задания. С учетом найденных значений (выражения
4.3 и 4.7), по отношению к заданию система обладает астатизмом первого порядка,
а по отношению к возмущению астатизмом не обладает (АIс = 0), т.е.
система статична. Для обеспечения требуемого астатизма необходимо, чтобы
регулятор скорости был ПИ-регулятором, для этого включим последовательно с
регулятором скорости интегратор, и чтобы не потерять устойчивость системы также
добавим форсирующее звено первого порядка, с единичным коэффициентом передачи.
Постоянная времени у интегратора и форсирующего звена равно 2(4T
), т.е. передаточная функция регулятора
скорости приобретет вид
,
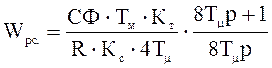(4.8)
В итоге получили ПИ-регулятор скорости, и условие астатизма выполняется.
4.11 Найдем по схеме 4.3 передаточную функцию (с учетом 4.8), получим
,
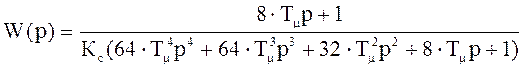(4.9)
4.12 Проверим выражение 4.9 с помощью грубого критерия устойчивости:
,
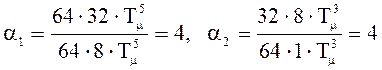(4.10)
Грубый критерий устойчивости указывает на устойчивость полученной системы.
4.13 Избавимся в схеме 4.1 от перекрестных связей и найдем передаточную функцию всей системы. Для этого точку съема тока перенесем из положения (1) в положение (2) (смотреть схему 4.1) и получим
 |
Схема 4.4 Преобразованная расчетная схема
4.13.1 Найдем передаточную функцию контура (I) (смотреть схему 4.4)
,
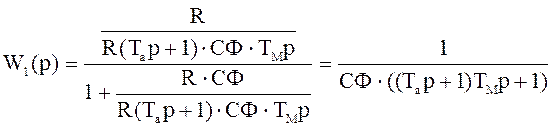(4.11)
4.13.2 Напишем формулы расчета передаточных функций для остальных контуров. Учтем, что компенсация по противоэдс является положительной обратной связью.
,
(4.12)
,
(4.13)
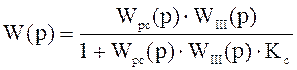, (4.14)
4.13.3 Пользуясь выражениями (4.11) – (4.14) и возможностями программы MathCAD получим передаточную функцию всей замкнутой системы
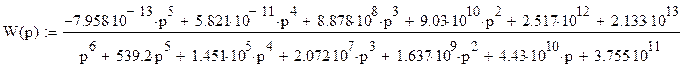, (4.15)
Как видно из выражения (4.15), необходимые условия устойчивости выполняются. Построим годограф Михайлова
|
|
|
|
Рисунок 4.1 Годограф Михайлова (а) –полное изображение,
(б) – увеличенное
Как видно из графиков (рис. 4.1) годограф Михайлова обходит в положительном направлении последовательно 5 квадрантов, при этом последовательность обхода не нарушается, что свидетельствует об устойчивых процессах в САУ (критерий устойчивости Михайлова).
5 АНАЛИЗ СИСТЕМЫ ПОДЧИНЕННОГО
РЕГУЛИРОВАНИЯ
5.1 Размыкаем систему и находим передаточную функцию разомкнутой системы
, (5.1)
5.2 Для определения запасов устойчивости воспользуемся критерием устойчивости Найквиста для ЛЧХ. Для этого построим логарифмические амплитудную и фазовую частотные характеристики (рис. 5.1).
|
|
|
|
Рисунок 5.1 Логарифмические частотные характеристики
Критерий устойчивости Найквиста для ЛЧХ, также
указывает на устойчивость системы, причем система имеет ненулевые запасы
устойчивости. По графикам определяем: 
рад, 
дБ, представленные запасы устойчивости менее
требуемых (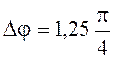
рад, 
дБ), но их можно считать удовлетворительными.
5.3 Пользуясь интегрированной программой MATLAB 6.1 (Simulink), смоделируем полученную систему и исследуем ее
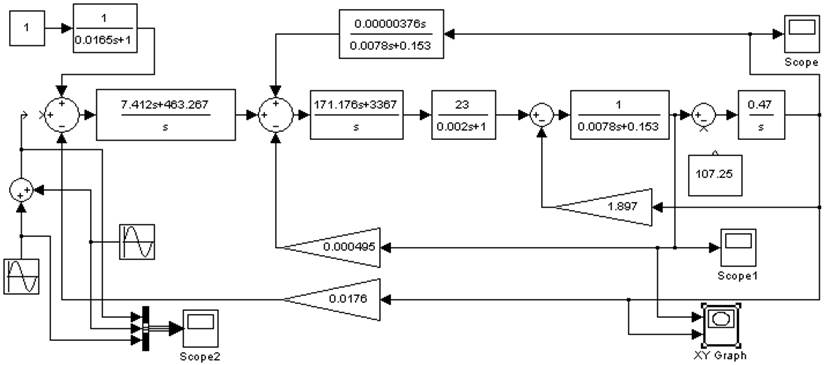
Схема 5.1 Исследуемая схема MATLAB 6.1 (Simulink)
5.4 Подаем на вход САУ единичный ступенчатый сигнал, строим графики изменения во времени угловой скорости и тока якоря двигателя.
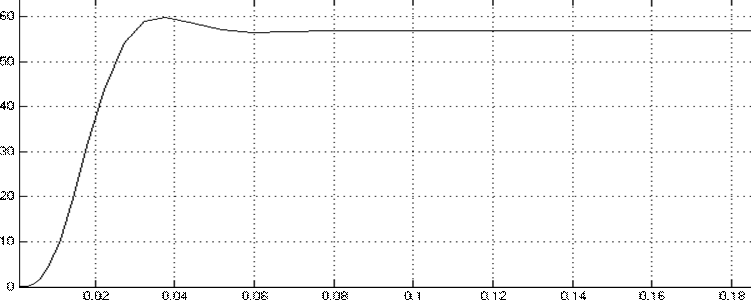
Рисунок 5.2 График изменения угловой скорости во времени w(t)
Рисунок 5.3 График изменения тока двигателя во времени i(t)
Стоит отметить, что единичный ступенчатый сигнал был
подан через апериодический фильтр, с единичным коэффициентом передачи и
постоянной времени Тф = 0,0165 с. Фильтр позволил добиться нужного
перерегулирования (по графику w(t): 
), при требуемом быстродействии (tр = 0,039 с).
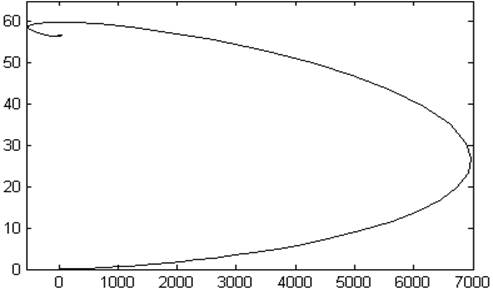
5.5 Результаты расчета представим в виде динамической электромеханической характеристики w(i)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
