Математическое описание и динамическая модель асинхронного двигателя. Регулирование напряжения на выходе двухзвенных преобразователей частоты, страница 5

Учитывая, что 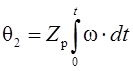, где – число пар полюсов машины, после вычисления производной и сокращения полученного уравнения           на , получим:

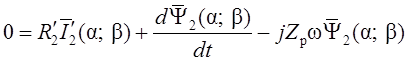.          (1.19)

Используя второе уравнение системы (1.6), приведем уравнение (1.19) к вращающейся системе координат:

.

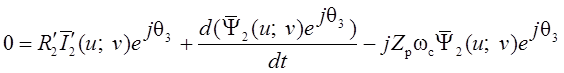Вычисляя производную и учитывая, что 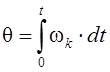, после сокращения     на , получим в окончательном виде:

.

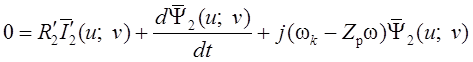В дальнейшем с целью упрощения аргументы в представлении векторов будем опускать и уравнения, описывающие электромагнитные процессы будем рассматривать в следующем виде:

1.7. Электромагнитный момент

Путем вычисления электромагнитной мощности, передаваемой        со стороны статора в воздушный зазор, в книге [11] показано, что электромагнитный момент, развиваемый двигателем, зависит от мнимой части векторного произведения векторов  и :

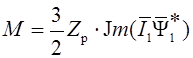.                               (1.20)

Здесь – вектор, сопряженный вектору .

Используя соотношения (1.17), выражение (1.20) можно представить также в следующих вариантах:

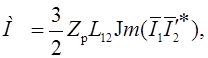
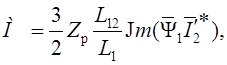
                          (1.21)

.

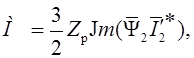
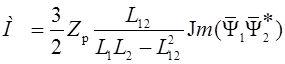1.8. Математические модели двигателя

При построении систем частотного управления асинхронным двигателем в большинстве случаев основными регулируемыми и контролируемыми координатами являются ток статора и потокосцепление ротора [5].  В связи с этим для описания формирования электрического момента, развиваемого двигателем, используем формулу (1.27). Тогда с учетом уравнения движения полную систему уравнений, описывающих асинхронный двигатель, можем записать следующим образом:

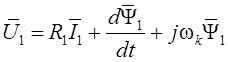,                                      (1.22)

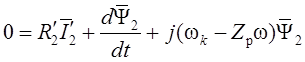,                         (1.23)

,                                                   (1.24)

,                                                  (1.25)

  ,                                       (1.26)

.                                                   (1.27)

Наилучший из способов частотного регулирования – управление       с поддержанием [11]. При этом механическая характеристика линейна, а электромагнитный момент ограничен лишь условиями насыщения главной магнитной цепи при увеличении скольжения.

Преобразуем систему (1.22–1.27), исключив  и .

Из (1.25)

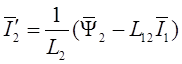.                                      (1.28)

Из выражений (1.28) и (1.24) получим:

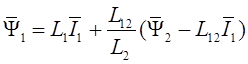.                           (1.29)

Подставив (1.29) в уравнение (1.22), можем записать:

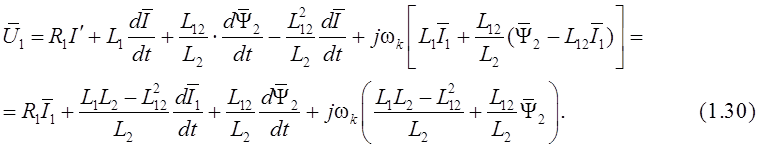
После подстановки выражения (1.28) в уравнение (1.23) получим:

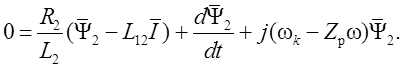                  (1.31)

Тогда 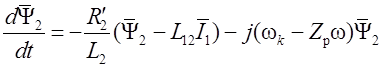 и выражение (1.30) можно представить в следующем виде:

Введем обозначения:

,

,

,

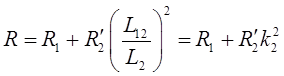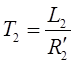и уравнения (1.31), (1.32) перепишем следующим образом:

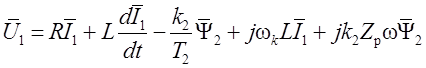,         (1.33)

.            (1.34)

Применяя к (1.33), (1.34) преобразование Лапласа, получим:

,              (1.35)

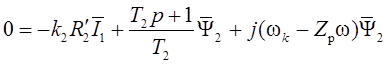,                   (1.36)

где .

Таким образом, метаматематическая модель двигателя описывается уравнениями (1.24–1.27), (1.35), (1.36).

При разложении обобщенных векторов по осям x и y системы координат, вращающейся со скоростью  вращения магнитного поля двигателя, полную систему уравнений, описывающих двигатель, получим       в следующем виде:

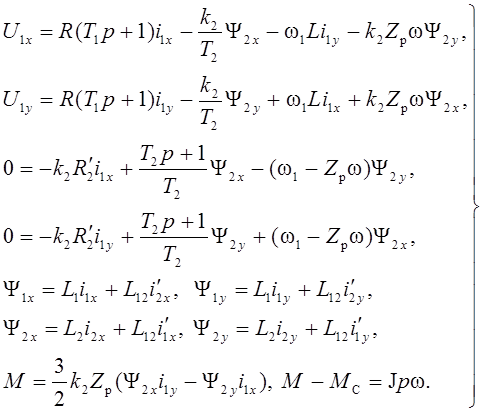
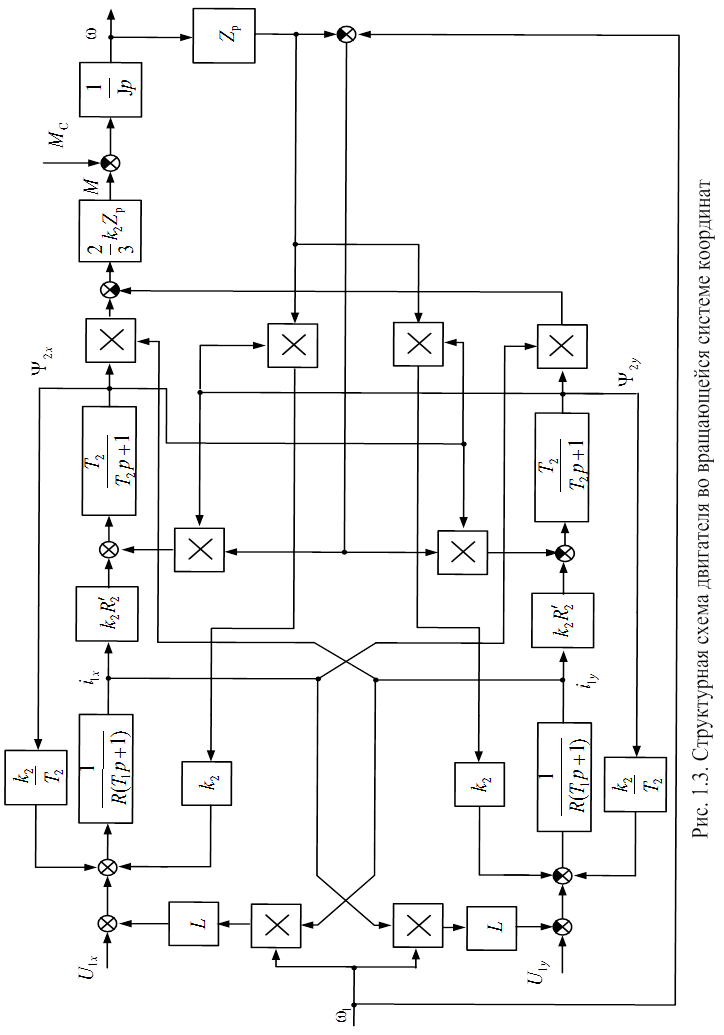
Соответствующая полученным уравнениям структурная схема приведена на рис. 1.3. Раскладывая обобщенные векторы по осям (α; β), получим систему уравнений:

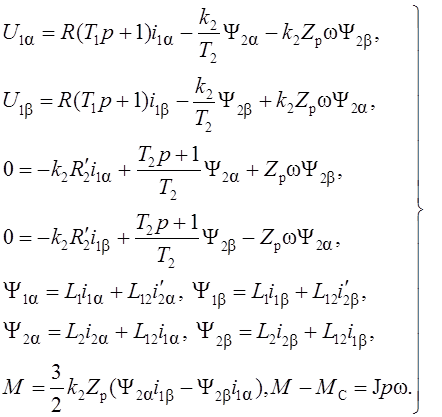
(1.37)

Структурная схема, построенная по уравнениям (1.37), приведена на рис. 1.4. При введении на рис. 1.3 и 1.4 структурные схемы характеризуют асинхронный двигатель с короткозамкнутым ротором как двумерный объект с внутренними перекрестными связями.

1.9. Математические модели двигателя при ориентации координатной системы по вектору потокосцепления ротора

В книге [11] показано, что при управлении с поддержанием  механическая характеристика двигателя является линейной, а развиваемый электрический момент ограничен лишь условиями насыщения главной магнитной цепи при увеличении скольжения. В связи с этим способ регулирования скорости при  в настоящее время является основным. Реализация указанного способа обеспечения при ориентировании вектора  по вещественной оси координатной системы.

При описании двигателя в системе (α; β) и ориентации оси α по вектору потокосцепления ротора имеем:

.

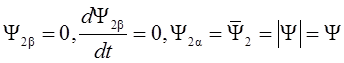В этом случае уравнения (1.37) упрощаются:

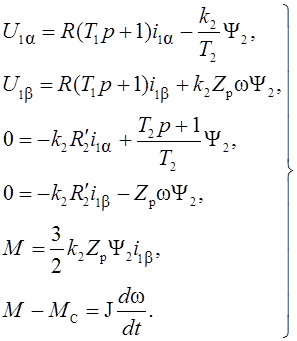                    (1.38)