![]() ,
, ![]() – индуктивности обмоток статора и ротора,
обусловленные потоком рассеивания;
– индуктивности обмоток статора и ротора,
обусловленные потоком рассеивания;
![]() – взаимоиндуктивность между обмотками статора и
ротора;
– взаимоиндуктивность между обмотками статора и
ротора;
θ2 – угол между одноименными осями обмоток статора и ротора;
![]() – угол между осями обмоток.
– угол между осями обмоток.
Так как рассматриваются приведенные к статору
значения токов и параметров ротора, т. е. предполагается одинаковое число
витков обмоток статора и ротора, то ![]() =
= ![]() =
= ![]() . В дальнейшем будем рассматривать уравнения (1.9), (1.10)
исходя из этого.
. В дальнейшем будем рассматривать уравнения (1.9), (1.10)
исходя из этого.
1.5. Преобразование исходных уравнений
Анализ уравнений (1.7–1.10) затрудняется рядом обстоятельств:
· уравнения (1.7) записаны для неподвижных обмоток, в то время как уравнения (1.8) – для обмоток, вращающихся со скоростью
ω вращения ротора;
· коэффициенты взаимоиндукции между обмотками статора и ротора в уравнениях (1.9), (1.10) являются функциями угла поворота ротора относительно статора, т. е. являются переменными коэффициентами.
Цель преобразования уравнений (1.7–1.10) заключается, во-первых, в приведении уравнений (1.7), (1.8) к одной системе координат (вращающейся или неподвижной), и, во-вторых, в преобразовании уравнений (1.9), (1.10) таким образом, чтобы они содержали только постоянные коэффициенты.
В отсутствии нулевых составляющих токов выполняются следующие условия:
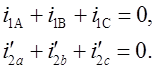
Тогда ![]() .
.
Так как угол между осями обмоток равен ![]() , то
, то
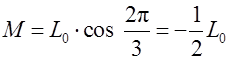 .
.
Следовательно,
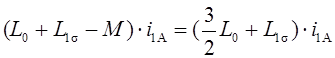 .
.
Индуктивность 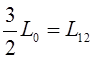 представляет
собой результирующую индуктивность, обусловленную магнитным потоком в воздушном
зазоре (главным потоком), создаваемым суммарным действием токов статора.
представляет
собой результирующую индуктивность, обусловленную магнитным потоком в воздушном
зазоре (главным потоком), создаваемым суммарным действием токов статора.
Эквивалентная индуктивность статора равна
![]() .
.
Аналогичные преобразования производятся и в двух других уравнениях системы (1.9), в результате чего получим выражения:
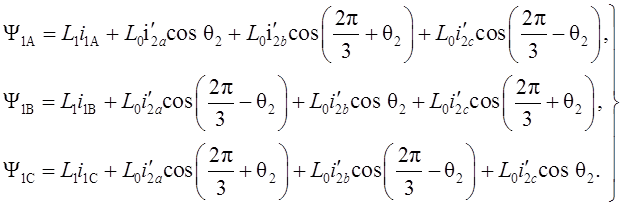 (1.11)
(1.11)
Уравнения (1.10) отличаются от уравнений (1.10) лишь индексами. Следовательно, систему (1.10) можно привести к следующему виду:
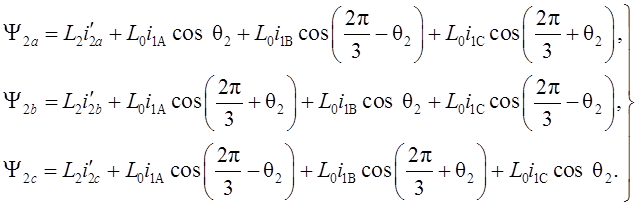 (1.12)
(1.12)
Умножим первое уравнение
системы (1.7) на ![]() , второе
–
, второе
– ![]() , третье – на
, третье – на 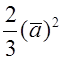 . Сложив
полученные выражения и учитывая (1.1), систему (1.12) можно записать в виде
одного уравнения
. Сложив
полученные выражения и учитывая (1.1), систему (1.12) можно записать в виде
одного уравнения
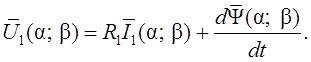 (1.13)
(1.13)
Здесь ![]() – результирующие
векторы напряжения, тока и потокосцепления, записанные в неподвижной системе
координат.
– результирующие
векторы напряжения, тока и потокосцепления, записанные в неподвижной системе
координат.
Аналогичным способом для ротора можно получить выражение
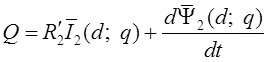 (1.14)
(1.14)
для обобщенных
векторов ![]() в системе координат
(d; q).
в системе координат
(d; q).
Умножим первое уравнение (1.11) на ![]() , второе –
, второе – ![]() , третье – на
, третье – на
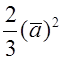 . Сложив
полученные выражения и проведя необходимые преобразования, получим:
. Сложив
полученные выражения и проведя необходимые преобразования, получим: 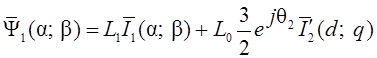 .
.
С учетом того, что 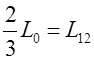 , имеем:
, имеем: ![]() .
.
Для представления вектора ![]() в неподвижной
системе координат воспользуемся вторым уравнением системы (1.6), заменив
систему (x; y) на систему (d; q).
Тогда
в неподвижной
системе координат воспользуемся вторым уравнением системы (1.6), заменив
систему (x; y) на систему (d; q).
Тогда
![]() . (1.15)
. (1.15)
Выполняя аналогичные действия по отношению к уравнениям (1.12), выражение для вектора потокосцепления ротора получим в следующем виде:
![]() . (1.16)
. (1.16)
Соотношения (1.15), (1.16) для потокосцеплений остаются справедливыми в общем случае системы координат, вращающейся с любой произвольной скоростью, если векторы токов статора и ротора описываются также в этой системе координат. С учетом этого выражения для потокосцепления можно записать в общем виде без указания системы координат:
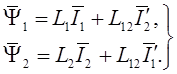 (1.17)
(1.17)
1.6. Приведение уравнений, описывающих электромагнитные процессы, к единой системе координат
Приведем уравнения (1.13), (1.14) к системе координат, в
общем случае вращающейся со скоростью ![]() . Для
преобразования уравнения (1.13) воспользуемся вторым выражением системы (1.6). Тогда
. Для
преобразования уравнения (1.13) воспользуемся вторым выражением системы (1.6). Тогда
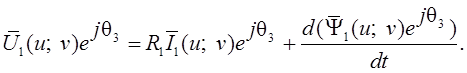 (1.18)
(1.18)
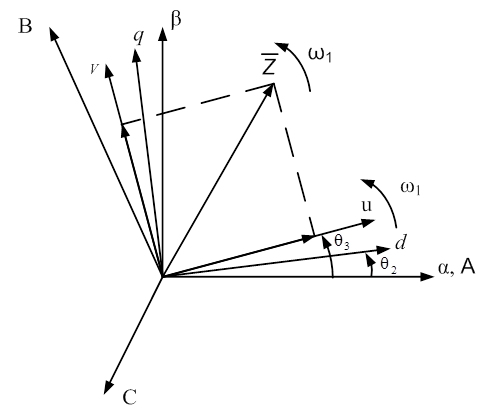
Рис. 1.2. Представление результирующего вектора
в системе координат (u; v)
Здесь ![]() – соответствующие
векторы, рассматриваемые в системе координат
– соответствующие
векторы, рассматриваемые в системе координат ![]() ;
; ![]() – угол поворота
координатной системы
– угол поворота
координатной системы ![]() относительно
системы
относительно
системы ![]() (рис. 1.2).
(рис. 1.2).
Применяя правило дифференцирования сложной функции, находим:
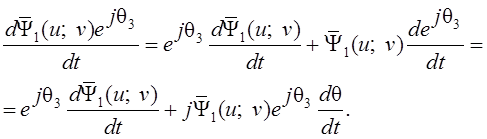
Учитывая, что 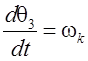 , после
подстановки вычисленной производной в (1.18) и сокращения на
, после
подстановки вычисленной производной в (1.18) и сокращения на ![]() , будем иметь
, будем иметь
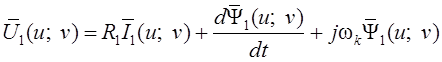 .
.
Так как система координат (d; q)
сдвинута относительно координат (α; β) на угол ![]() , то согласно первому уравнению системы (1.6)
, то согласно первому уравнению системы (1.6)
![]() ,
, ![]() .
Тогда уравнение (1.14) можно представить в следующем виде:
.
Тогда уравнение (1.14) можно представить в следующем виде:
 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.