Математическое описание и динамическая модель асинхронного двигателя. Регулирование напряжения на выходе двухзвенных преобразователей частоты, страница 2

– магнитодвижущие силы обмоток и магнитные поля расположены вдоль окружности воздушного зазора по синусоидальному закону;

– воздушный зазор равномерный вдоль расточки статора;

– реальная распределенная обмотка заменена эквивалентной сосредоточенной, создающей ту же намагничивающую силу;

– потери в стали отсутствуют;

– напряжение и токи не содержат нулевые последовательности;

– индуктивные сопротивления рассеяния, цепи намагничивания неизменны и не зависят от положения ротора относительно статора.

1.2. Двухфазные системы координат для описания трехфазной

асинхронной машины

Математическое описание трехфазного двигателя основано на эквивалентном преобразователе этой машины на двухфазную. В книге [8] показано,  что любую трехфазную систему переменных состояний (напряжений, токов, потокосцеплений) можно представить в виде результирующего вектора, вращающегося в положительном направлении со скоростью, пропорциональной частоте питающего напряжения. В каждый момент времени проекции результирующего вектора на магнитные оси обмоток дают мгновенные значения переменных на оси этих обмоток.

Результирующие векторы можно разложить также на две взаимно ортогональные проекции. Это эквивалентно представлению трехфазной машины в виде двухфазной, потому что как для исходного трехфазного, так  и для абстрактного двухфазного результирующие векторы будут           совпадать.

В теории электроприводов переменного тока с частотным регулированием рассматриваются 4 варианта систем координат, с использованием которых трехфазная машина преобразуется в эквивалентную двухфазную: (α; β), (x; y), (u; v), (d; q). Каждая из этих систем отличается от других значением ω_k скорости вращения координатной системы.

Система координат (α; β) неподвижна относительно статора, т. е. ее скорость вращения равна нулю (ω_k = 0). При этом вещественная ось α направлена по оси обмотки фазы А.

Система (x; y) вращается в положительном направлении синхронно     с магнитным полем машины (ω_k = ω₁), ось x является вещественной. Система (u; v) вращается также в положительном направлении с произвольной скоростью ω_k. Ось u – вещественная. Система координат (d; q) жестко связана с ротором, т. е. скорость вращения этой системы равна скорости вращения ротора: ω_k = ω.

При построении асинхронных электроприводов с частотным управлением нашли применение системы координат (α; β), (x; y).

1.3. Соотношения между переменными состояния

 в различных системах координат

Решение задачи преобразования переменных состояния трехфазной машины к переменным двухфазной модели этой машины должно выполнятся с учетом инвариантности мощности.

Условие инвариантности мощности при преобразовании переменных состоит в том, что суммарная мгновенная мощность, потребляемая обмотками статора трехфазного двигателя, должна быть равной мощности,      потребляемой эквивалентной двухфазной машиной.

В книге [8] показано, что если для некоторой трехфазной переменной состояния Z известны мгновенные значения Z_A(t)_, Z_B(t)_, Z_C(t)_, то результирующий вектор можно определить исходя из выражения

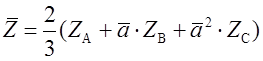, где 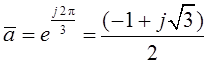,  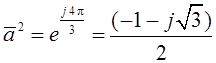– коэффициенты, преобразующие скаляры  в векторы.

Введем согласующий коэффициент пропорциональности k_c, обеспечивающий выполнение условий инвариантности мощности при трехфазно-двухфазных преобразованиях, с учетом которого

.                         (1.1)

При

                    (1.2)

из (1.1) следует, что

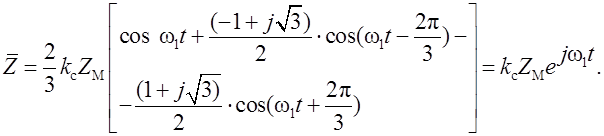
Следовательно, результирующий вектор

является вектором с модулем , вращающимся в положительном направлении со скоростью , где f₁ – частота питающего напряжения. Проекции этого вектора на оси А, В, С фазных обмоток статора пропорциональны (с коэффициентом пропорциональности k_c) мгновенным значением переменной состояний Z.

Рассмотрим преобразование трехфазной системы координат (А, В, С) в двухфазную систему (α; β). При разложении вектора  по ортогональным осям α; β его проекция на ось α представляет собой вещественную,     а проекция на ось β мнимую части.

В соответствии с (1.1)

При отсутствии нулевой последовательности в разложении трехфазной системы _{, ,}  для любого момента времени выполняется условие . Следовательно, . Тогда