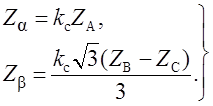Математическое описание и динамическая модель асинхронного двигателя. Регулирование напряжения на выходе двухзвенных преобразователей частоты, страница 3

                                  (1.3)

Если переменные состояния, ,  описываются выражениями (1.2), то

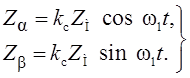                                    (1.4)

Таким образом, переменные состояния трехфазной системы , ,  являющиеся гармоническими сигналами, в координатной системе (α; β) также являются гармоническими сигналами.

При разработке систем регулирования и моделировании переходных процессов возникает необходимость обратного преобразования из системы (α; β) в систему (A, B, C). Для получения необходимых соотношений используем уравнения (1.4). Проекция  вектора на ось обмотки фазы А определяется непосредственно из первого выражения системы (1.4).

При определении проекций  и  учтем, что . Тогда второе выражение в (1.3) можно записать следующими способами:

,

.

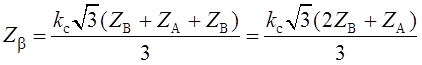Следовательно,

                                 (1.5)

Для определения согласующего коэффициента k_с, обеспечивающего выполнение условия инвариантности мощности при преобразовании переменных, определим мгновенные мощности, потребляемые обмотками статора трехфазного двигателя и обмотками эквивалентной двухфазной машины.

Мощность, потребляемая трехфазной машиной, равна

.

Определив составляющие  и  обобщенных векторов           напряжения         

 

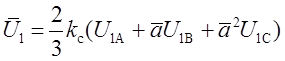
и токов      

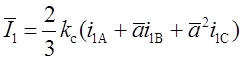
в соответствии с выражениями (1.5), получим:

Две статорные обмотки эквивалентного двухфазного двигателя потребляют мощность, равную .

Следовательно, условие инвариантности мощности при трехфазно-двухфазном и двухфазно-трехфазном преобразовании переменных выглядит следующим образом:

.

Отсюда следует, что согласующий коэффициент равен

.

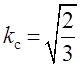Если результирующий вектор , рассматриваемый в трехфазной системе координат , обозначим как , а тот же вектор     в системе (α; β) как (α; β), то упрощенно рассмотренные преобразования A, B, C /α; β и α; β /A, B, C можно записать в виде (α; β)      и (α; β)  .

Для вычисления проекций Z_x, Z_y вектора рассмотрим преобразование вектора (α; β) в вектор (x; y), представляющим собой обобщенный вектор , рассматриваемый в системе координат (x; y), вращающейся       со скоростью вращения магнитного поля .

Если система координат (x; y) повернута относительно системы (α; β) на угол , а вектор  повернут относительно оси α на угол φ (см. рис. 1.1), то справедливы соотношения:

, .

Следовательно, для преобразования (α; β)  (x; y), (x; y)  (α; β) получаем следующие выражения:

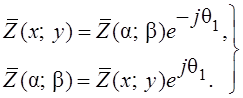                             (1.6)

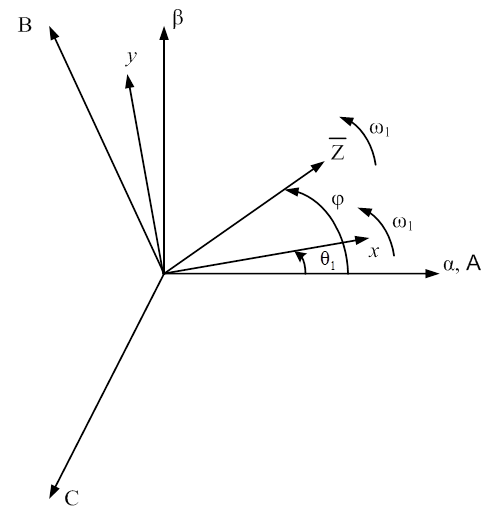
Рис. 1.1. Представление обобщенного вектора

в неподвижной и вращающейся системах координат

Учитывая, что , , из первого уравнения системы (1.6) получим:

,

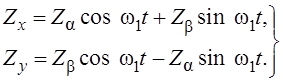
Если ,, то

В частном случае, когда φ₀ = 0, чему соответствуют уравнения (1.4), , .

Из рассмотренного следует, что в координатной системе (x, y) переменные состояния двигателя не содержат гармонических сигналов,            т. е. представляются в виде сигналов постоянного тока.

Из уравнений (1.3), (1.6) можно получить выражение для преобразования (α; β) в следующем виде:

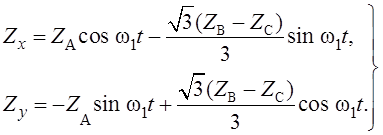
Преобразование выполняется на основе второго уравнения системы (1.7) и описывается выражениями

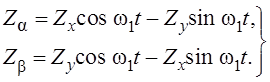
1.4. Исходные уравнения, описывающие

электромагнитные процессы

Уравнения баланса ЭДС в цепях статора и ротора базируются на втором законе Кирхгофа и записываются следующим образом:

                                     (1.7)

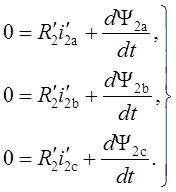                                        (1.8)

Здесь R₁ – активные сопротивления фазных обмоток статора;  – токи в статорных обмотках; – потокосцепления обмоток статора;  – приведенные к статору активные сопротивления фаз ротора;  – приведенные токи ротора;  – потокосцепления фаз ротора.

Следует подчеркнуть, что уравнения (1.7) записаны в трехфазной системе координат, жестко связанной с неподвижным статором, а уравнения (1.8) – в трехфазных координатах, жестко связанных с ротором.

Потокосцепление каждой обмотки зависит от токов во всех обмотках. Для статора получим систему [7]:

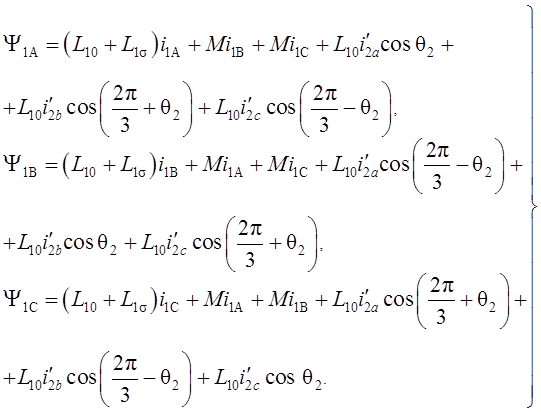        (1.9)

Аналогичным образом для ротора можно записать:

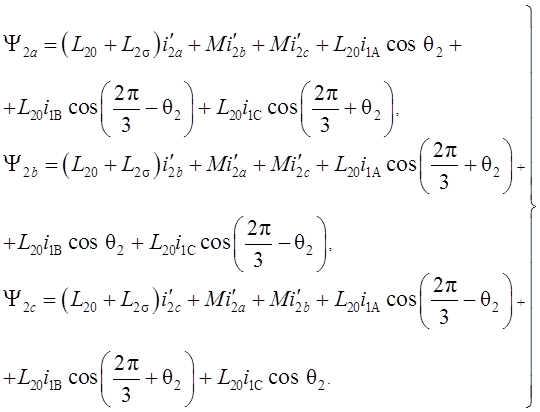         (1.10)

В выражениях (1.9), (1.10) приняты следующие обозначения:

,  – соответственно индуктивности обмоток статора и ротора, обусловленные основным потоком;