Компьютерное моделирование и анализ кинематики плоских рычажных механизмов, страница 8

Затем, зная кинематические характеристики D, принимая начало направляющей ползуна E в точке C, угол наклона, аналог угловой скорости и аналог углового ускорения направляющей равными нулю, зная длину шатуна DE (звено 4) и длину звена 5, обращаемся к процедуре для группы Ассура второго вида         diada2v(dx,dy,vdx,vdy,adx,ady,cx,cy,0,0,0,0,0,0,0,l4,0,fi4,om4,epsi4,l5,v5,a5);.

Последние шесть параметров данной процедуры являются выходными, следовательно определены положение, аналог угловой скорости и аналог углового ускорения звена 4, а также положение ползуна (звено 5), его аналоги скорости и ускорения.

Таким образом, для данного положения начального звена определены все кинематические характеристики механизма. Как уже отмечалось, вывод полученных результатов кинематического анализа нагляднее всего представить графически.

Построение положения механизма начнем с задания положения абсолютной системы координат XAY. Обращаемся к вспомогательной процедуре CoordXY(100,200) и строим координатные оси в точке А(100,200) пикселей. Затем, обращаясь к процедуре Opora, строим условное обозначение опоры. Определяем в пикселях координаты точки B и строим линию AB   x1 := ox + round(kl*bx); {kl - масштабный коэффициент длины}   y1 := oy - round(kl*by);

MoveTo(ox,oy);           {переход в начало системы координат}   LineTo(x1,y1);           {линия AB}.

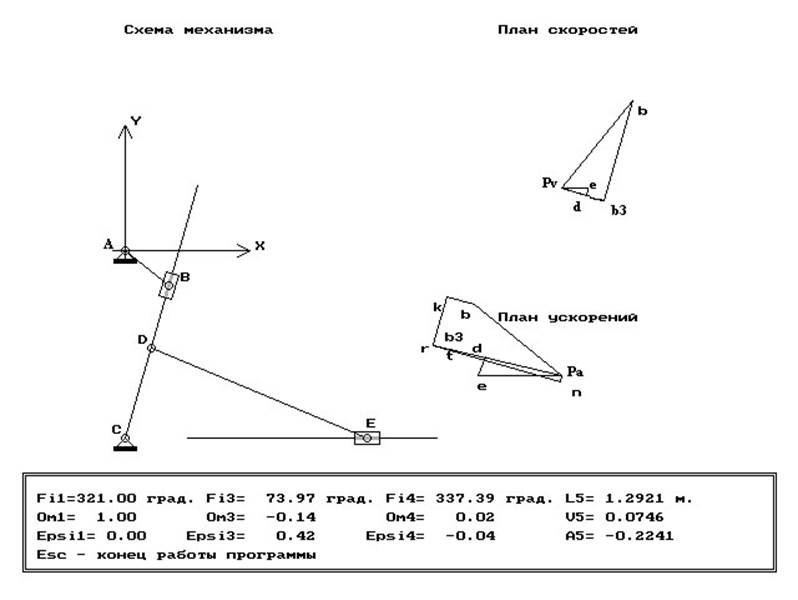
Рис. 6

Далее определяем положение точки C, строим опору и проводим линию наклона кулисы

MoveTo(ox,oy - round(kl*cy));

Circle(ox,oy - round(kl*cy),3);   Opora(ox,oy - round(kl*cy));

x1 := ox + round(kl*l30*cos(fi3)); {l30 - длина кулисы}   y1 := oy - round(kl*cy) - round(kl*l30*sin(fi3));   LineTo(x1,y1);  {линия наклона кулисы}.

Зная координаты точки B, строим при помощи вспомогательной процедуры

PostPara положение поступательной пары B под углом наклона ϕ₃   Postpara(ox + round(kl*bx),oy - round(kl*by),fi3);.

Определяем координаты точки D и показываем  ее положение

x1 := ox + round(kl*dx); y1 := oy - round(kl*dy);   Circle(x1,y1,3);.

Далее определяем координаты точки E, проводим линию DE, линию направляющую ползуна E, строим поступательную и вращательную пары в точке E   MoveTo(x1,y1);

x2 := x1 + round(kl*l4*cos(fi4));   y2 := y1 - round(kl*l4*sin(fi4));   LineTo(x2,y2); {линия DE}

Line(ox + 50, y2, ox + 250, y2);  {линия направляющей ползуна E}   Postpara(x2,y2,0);  {поступательная пара E}   Circle(x2,y2,3);    {вращательная пара E}.

2.3  Построение планов скоростей механизма

Выбираем координаты полюса плана скоростей pvx,pvy. Далее строим аналог скорости точки В_1,2   x1 := pvx + round(kv*vbx);   {kv - масшт. коэффициент скорости}   y1 := pvy - round(kv*vby);

Line(pvx, pvy, x1, y1);  {аналог скорости Vb_1,2}.

Далее проводим аналоги относительной Vb_3,2 и абсолютной Vb₃ скоростей   x2 := x1 - round(kv*v3*cos(fi3));   y2 := y1 + round(kv*v3*sin(fi3));

Line(x1,y1,x2,y2);  {аналог относительной скорости Vb_3,2}   Line(pvx,pvy,x2,y2); {аналог абсолютной скорости Vb₃}. Определяем аналоги скоростей точек E и D

x1 := pvx + round(kv*v5);

y1 := pvy;

Line(pvx, pvy, x1, y1); {аналог скорости точки E}   x2 := pvx + round(kv*vdx);

y2 := pvy - round(kv*vdy);

Line(x1,y1,x2,y2);  {аналог относительной скорости Ved}.

2.4  Построение планов ускорений механизма

Выбираем координаты полюса плана ускорений pax,pay. Проводим линию аналога ускорения точки B_1,2   x1 := pax + round(ka*abx);  {ka - масштабный коэффициент}

y1 := pay - round(ka*aby);  {аналога ускорения}   Line(pax,pay,x1,y1);        {аналог ускорения B_1,2}.

Затем строим аналоги ускорений Кариолиса и релятивного

x2 := x1 + round(ka*2*v3*om3*sin(fi3));   y2 := y1 + round(ka*2*v3*om3*cos(fi3));

Line(x1,y1,x2,y2);          {аналог ускорения Кариолиса}   x1 := x2 - round(ka*a3*cos(fi3));   y1 := y2 + round(ka*a3*sin(fi3));