Компьютерное моделирование и анализ кинематики плоских рычажных механизмов, страница 2

Все библиотечные процедуры имеют входные параметры в виде координат, аналогов скоростей и ускорений внешних кинематических пар и вычисляют положения звеньев, образующих внутреннюю кинематическую пару, их аналоги скоростей и ускорений. Переход от аналогов скоростей и ускорений к действительным скоростям и ускорениям не вызывает затруднений:

V_i =S_i^’*ω₁;   A_i = S_i^’’*ω₁²;

Здесь V_i - скорость i-го звена,

S_i^’  - аналог скорости (передаточная функция) i-го звена,

ω₁   - угловая скорость начального звена,       A_i   - ускорение i-го звена,

S_i^’’  - аналог ускорения i-го звена.

Необходимо отметить, что вышеприведенные соотношения справедливы только при постоянной угловой скорости начального звена. Так как кинематическое исследование предполагает постоянство угловой скорости такого звена, то данные определения аналогов скоростей и ускорений вполне корректны.

Компьютерное исследование кинематики механизма наиболее просто можно осуществить следующим образом: циклически задавая положение начального звена, обращаемся к процедуре, рассчитывающей кинематические характеристики группы Ассура, связанной с начальным звеном и стойкой механизма, затем определяем характеристики точки данной группы, кинематически связанной с последующей группой Ассура и обращаемся к соответствующей процедуре и т.д..

Работая в графическом режиме работы компьютера, можно сравнительно просто организовать имитацию движения механизма. Зная проекции аналогов скоростей и ускорений всех звеньев механизма, построить планы скоростей и ускорений в каждом положении механизма. Если необходимы значения кинематических характеристик, их можно вывести на дисплей.

1.  ОПРЕДЕЛЕНИЕ КИНЕМАТИЧЕСКИХ ХАРАКТЕРИСТИК ГРУПП АССУРА

1.1  Группа Ассура первого вида (2ПГ1В)

1.1.1  Положения звеньев

Положения звеньев данной группы Ассура определим с помощью рис. 1, на котором представлена схема группы в соответствующей системе координат, обозначения звеньев и кинематических пар. Назовем конфигурацию группы сборкой № 1 когда координата точки B в локальной системе координат x₁o₁y₁ B_y1 > 0, в противном случае мы имеем сборку № 2. Известны координаты точек A,C в абсолютной системе координат, длины звеньев l₂ и l₃ и необходимо определить абсолютные координаты точки B, углы φ₂ и φ₃. Расстояние AC определим по теореме Пифагора

AC = (C_x − A_x)² +(C_y − A_y)² .

Угол α определим по формуле

C_y − A_y  α= arctan _Cx _{− A}x _ , а для определения локальных координат B_x1 и B_y1 воспользуемся теоремой косинусов и теоремой Пифагора. Учитывая, что B_x1 = l₂cos∠BAC, получаем

l2² + AC² −l3²                                        2               2

                                                                Bx1 =                        ,     By1 = l2 − Bx1 .

2AC

Здесь необходимо отметить, что если конфигурация группы Ассура соответствует сборке № 2, то By₁ = - By₁.

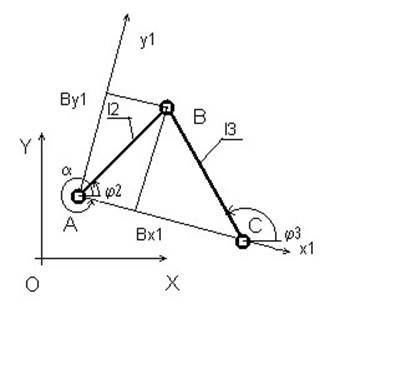
Рис. 1

Теперь совсем просто можно определить абсолютные координаты точки B, используя метод преобразования координат:

B_x = A_x + B_x1 cosα− B_y1 sinα

By = Ay + Bx1 sinα+ By1 cosα.

Затем определяем углы наклона звеньев l₂,l₃ - ϕ₂ и ϕ₃

 B_y − A_y                                     B_y −C_y 

ϕ₂ = arctan _Bx ₋ Ax _                     ϕ₃ = arctan_ Bx ₋Cx _ .

Так как все углы отсчитываются от положительного направления оси X, то в библиотеку процедур включена специальная функция, вычисляющая угол в радианах в любой четверти через арктангенс (Atan2). Более того, все вычисления углов в процедурах осуществляются при помощи этой функции.

1.1.2  Аналоги скоростей

Для определения аналогов скоростей воспользуемся методом замкнутых векторных контуров и напишем проекции векторного уравнения на координатные оси

_AA^x_y ++l_l²2 ^cos_sinϕ^ϕ2² ₌⁼_C^C_y^x ₊⁺_l^l3³_sin^cos_ϕ^ϕ3³_.                                                 (1)