Компьютерное моделирование и анализ кинематики плоских рычажных механизмов, страница 4

ll22 cossinϕϕ22−−ll44sincosϕϕ33==CCyx−−AAyx+−ll33cossinϕϕ33 .                                  (9)

Произведя дифференцирование данной системы уравнений по ϕ₁ и простейшие преобразования, получим линейную систем уравнений, в которой неизвестными являются ω₂ и V₄

ω−2 2ωl2 2cosl sinϕϕ2 −2 −V4Vsin4 cosϕ3ϕ=3 =VcVcy −x Va−Vay −x ω−ω3 3(l3 3(lsincosϕ3ϕ−3 l+4 cosl4 sinϕ3ϕ)3).                         (10)

Решение данной системы уравнений получим в виде

b1       a12                                                   a11      b1

                                            ω₂ = _a^b11^{2                                       a}_a²²12               V₄ = _a^a11²¹ _a^b1²2 ,                               (11)

a21      a22                                                a21      a22

где

aa1121 = −= l2lcos2 sinϕϕ22               aa1222 = −= −cossinϕϕ33                bb12 ==VcVcxy −−VaVaxy+−ωω3 4 223 4((l al a12 +−l al a33 2212)).         (12)

1.2.3  Аналоги ускорений

Дважды продифференцировав (9) и проведя небольшие преобразования, получим значения аналогов ускорений ε₂ и A₄

b1      a12                                              a11      b1

                                       ε₂ = _a^b11^{2                                             a}_a²²12            A₄ = _a^a11²¹ _a^b1²2 ,                                      (13)

a21       a22                                           a21      a22

где a₁₁,a₁₂,a₂₁,a₂₂ определяются из (12), а b₁,b₂ вычислим следующим образом:

b1 = Acx − Aax −ω32(l4 cosϕ3 − l3 sinϕ ω3)+ 22l2 cosϕ2 − 2V4 3ω ϕ εsin 3 − 3 4(l sinϕ3 + l3 cosϕ3) b₂ = Ac_y − Aa_y −ω₃²(l₄ sinϕ₃ + l₃ cosϕ ω₃)+ ₂²l₂ sinϕ₂ + 2V_{4 3}ω ϕ εcos ₃ + _{3 4}(l cosϕ₃ − l₃ sinϕ₃⁾.   14)

1.3  Группа Ассура третьего вида (2ПГ3В)

1.3.1  Положения звеньев

Положения звеньев данной группы можно определить, воспользовавшись данными рис. 3. Длину активной части кулисы l₃ определим из выражения

                                        l₃ = (A_x − C_x)² +(A_y − C_y)² − l₂² ,                                       (15)

где координаты точек A,C и длина второго звена l₂ известны. Угол наклона кулисы ϕ₃ определим из выражения

ϕ₃ = arctan^_ ^A_Ax^{y −}_{− C}^Cx^y_^ − arctan^_ ^l_l²3_^ .                                     (16)

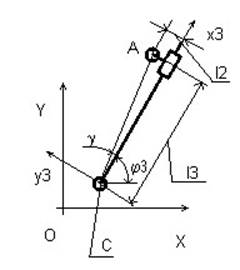
Рис. 3

1.3.2  Аналоги скоростей

Запишем проекции векторных уравнений замкнутых контуров на оси координат X,Y в следующем виде:

_ll³3 ^cos_sinϕ^ϕ3³₊⁻_l^l2²_cos^sinϕ_ϕ³3 ⁼₌ ^A_A^xy ⁻₋ ^C_C^xy.                                    (17)

Продифференцировав (17) по ϕ₁, получим, после небольших преобразований, систему уравнений

a Va V1121 33 ++ aa122 32 3ωω == bb12,                                            (18) где

aa1121 == cossinϕϕ33     aa1222 = −= l3(cosl3 sinϕ3ϕ−3 l+2 sinl2 cos )ϕ33   bb12 ==VaVaxy −−VcVcxy.               (19)

Следовательно, можно легко получить значения аналогов скоростей V₃ и ω₃

b1       a12                                       a11      b1

                                                V₃ = _a^b11^{2                                        a}_a²²12         ω₃ = _a^a11²¹ _a^b1²2 .                                 (20)

a21      a22                                     a21       a22

1.3.3  Аналоги ускорений

Продифференцировав дважды (17) по ϕ₁ и решив полученную систему уравнений, имеем:

b1       a12                                       a11      b1

                                             A₃ = _a^b11^{2                                                a}_a²²12         ε₃ = _a^a11²¹ _a^b1²2 ,                                    (21)

a21      a22                                    a21       a22

где a₁₁,a₁₂,a₂₁,a₂₂ определяются из (19), а b₁,b₂ - по следующим выражениям:

b1 = Aax − Acx + 2V3 3 2ωa 1 + a22 3ω2