Компьютерное моделирование и анализ кинематики плоских рычажных механизмов, страница 3

Продифференцируем полученные уравнения по обобщенной координате ϕ₁. Учитывая, что нам известны значения аналогов скоростей точек A и C

(Va_x,Va_y,Vc_x,Vc_y), а также значения углов ϕ₂,ϕ₃, получим линейную систему двух уравнений

_ωω^{2 2}2 2ll ^sin_cos^ϕ_{ϕ ω}²2 ⁻₋^{ω3 3}3 3^l_l ^sin_cos^ϕ_ϕ³3⁼₌^Va_Vc^xy ⁻₋^Vc_Va^xy_,                                          (2)

где неизвестными являются аналоги скоростей ω₂,ω₃. Решение данной системы линейных уравнений проведем методом Крамера. В этом случае представляем уравнения в виде

_aa¹¹21^ω_ω²2 ⁺₊^a_a¹22 3^{2 3ω}_ω ⁼₌ ^b_b¹2 ,                                                  (3)

где коэффициентами a₁₁,a₁₂,a_21,a₂₂,b₁,b₂ представлены следующие постоянные, известные нам по значениям, выражения:

a11 = −l2 sinϕ2           a12 = l3 sinϕ3      b1 = Vcx −Vax a21 = l2 cosϕ2     a22 = −l3 cosϕ3     b2 = Vcy −Vay.

Тогда

b1       a12                                      a11      b1

                                             ω₂ = _a^b11^{2                                            a}_a²²12        ω₃ = _a^a11²¹ _a^b1²2 .                                      (4)

a21      a22                                    a21       a22

1.1.3  Аналоги ускорений

Для получения аналогов ускорений дважды продифференцируем уравнения (1) по ϕ₁:

Aax −ω22l2 cosϕ ε2 − 2 2l sinϕ2 = Acx −ω32l3 cosϕ ε3 − 3 3l sinϕ3

Aay −ω22l2 sinϕ ε2 + 2 2l cosϕ2 = Acy −ω32l3 sinϕ ε3 + 3 3l cosϕ3. Преобразуем полученные выражения к виду (3)

a11ε2 + a12 3ε = b1 a21ε2 + a22 3ε = b2, где коэффициенты a₁₁,a₁₂,a₂₁,a₂₂ сохраняют свои старые значения, а b₁,b₂ определяются по следующим зависимостям:

b1 = Acx − Aax + a21ω22 + a22 3ω2        b2 = Acy − Aay − a11ω22 − a12 3ω2 .

В этом случае, аналоги ускорений ε₂,ε₃ будут равны:

b1       a12                                           a11      b1

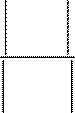
                                           ε₂ = _a^b11^{2                                         a}_a²²12            ε₃ = _a^a11²¹ _a^b1²2 .                                     (5)

a21      a22                                         a21       a22

1.2  Группа Ассура второго вида (2ПГ2В)

1.2.1  Положения звеньев

Схема данной группы Ассура, координатная система и обозначения кинематических пар и звеньев представлены на рис. 2.

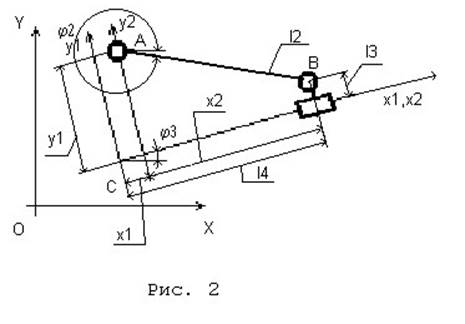
Вычислим координаты точки A в локальной системе координат X₁CY₁

CCxy ++ AAxx11 cossinϕϕ33+− AAyy11 cossinϕϕ33 == AAxy.                                           (6)

В выражении (6) нам известны абсолютные координаты точек A,C, а также угол наклона направляющей для поступательной пары группы - ϕ₃. К числу неизвестных, подлежащих определению, относятся координаты точки А в локальной системе координат X₁CY₁. Перенеся C_x и C_y в правую часть, получим линейную систему двух уравнений, решение которой представим в виде:

b1 − sinϕ3                                                      cosϕ3      b1

                             A_x1 = _cos^b2_ϕ3 ^co₋^s_sin^ϕ3_ϕ3         A_y1 = _cos^sin_ϕ3^ϕ3_{− sin}^b2_ϕ3 .                          (7)

sinϕ₃         cosϕ₃                                           sinϕ₃         cosϕ₃

Здесь b₁ = A_x - C_x  и  b₂ = A_y - C_y. Так как определители знаменателей в (7) равны 1, то значения неизвестных равны значениям определителей, расположенных в числителях

A_x1 = b₁ cos^ϕ₃ + b₂ sin^ϕ₃            A_y1 = b₂ cos^ϕ₃ −b₁sin^ϕ₃. Далее определяем x₂ - проекцию звена 2 на направляющую

x2 = l22 −(Ay1 − l3)2 , а затем и длину направляющей CB

l₄ = A_x1 + x₂.

Абсолютные координаты точки B и угол наклона звена l₂ определяем по следующим выражениям:

BBxy == CCxy ++ ll44 cossinϕϕ33+−ll33cossinϕϕ33          ϕ2 = arctan BBxy −− AAxy .                     (8)

1.2.2  Аналоги скоростей

Для определения аналогов скоростей напишем проекции замкнутых векторных контуров на координатные оси X и Y