Компьютерное моделирование и анализ кинематики плоских рычажных механизмов, страница 5

b2 = Aay − Acy − 2V3 3ωa11 − a12 3ω2.                                (22)

1.4  Группа Ассура четвертого вида (2ПГ4В)

1.4.1  Положения звеньев

Положения звеньев данной группы Ассура определим по рис. 4, на котором приведены обозначения звеньев и кинематических пар.

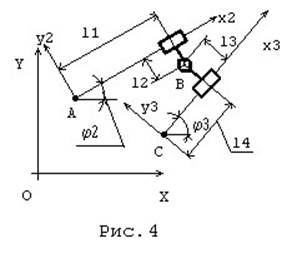
Запишем систему уравнений замкнутого контура в проекциях на координатные оси X,Y

AAxy ++ll11cossinϕϕ22 +−ll22cossinϕϕ22 == CCxy ++ll44cossinϕϕ33+−ll33cossinϕϕ33.                            (23)

Неизвестными в данных выражениях являются l₁,l₄, а остальные данные передаются в процедуру и являются известными. Полученная система уравнений является линейной относительно неизвестных. Запишем решение этой системы в виде:

b1       a12                                               a11      b1

                                                l₁ = _a^b11^{2                                     a}_a²²12              l₄ = _a^a11²¹ _a^b1²2 ,                             (24)

a21       a22                                             a21      a22

где коэффициенты a₁₁,a₁₂,a₂₁,a₂₂,b₁,b₂     определяются по выражениям:

aa1121 == cossinϕϕ22       aa1222 = −= −cossinϕϕ33      bb12 == CCxy −− AAxy+−l al a2 22 111 +−l al a3 223 12.             (25)

1.4.2  Аналоги скоростей

Продифференцировав систему уравнений (23) по ϕ₁, получим после простых преобразований:

b1       a12                                               a11      b1

                                                  V₁ = _a^b11^{2                               a}_a²²12             V₄ = _a^a11²¹ _a^b1²2 ,                          (26)

a21      a22                                             a21      a22

где a₁₁,a₁₂,a₂₁,a₂₂ определяются из (25), а b₁,b₂ - по выражениям:

bb1₂ ==VcVcxy −−VaVaxy+−ωω2₂((l al a11 1121 +−l al a22 2111))+−ωω3 4 223 4((l al a12 +−l al a33 2212)).                  (27)

1.4.3  Аналоги ускорений

Дважды продифференцировав (23) по ϕ₁, можно получить

b1       a12                                                a11      b1

                                             A₁ = _a^b11^{2                                        a}_a²²12             A₄ = _a^a11²¹ _a^b1²2 ,                                (28)

a21       a22                                              a21       a22

где a₁₁,a₁₂,a₂₁,a₂₂ определяются из (25), а b₁,b₂ - по выражениям:

b1 = Acx − Aax + 2V1ω2 2a 1 +ω22(l a1 11 − l a2 21)+ε2(l a1 21 + l a2 11)

bb12 = b1 +y2V4 3 22ωya +ω32(l a4 12 −2l a3 22(l a1 2)1++εl a3 4 222(l a11)−ε+2l a(3l a1 1112) − l a2 21).              (29)

= Ac − Aa − 2V1ω2a11 +ω2

b2 = b2 − 2V4 3ω a12 +ω32(l a4 22 + l a3 12)−ε3 4(l a12 − l a3 22)

1.5  Группа Ассура пятого вида (2ПГ5В)

1.5.1  Положения звеньев

Положения звеньев определим с помощью рис. 5, где приведена схема группы, обозначения звеньев и кинематических пар и система координат. Напишем проекции замкнутого векторного контура на координатные оси X,Y

Ax = Cx + Bx3 cosϕ3 + Ax2 cos(ϕ α3 + )−l2 sin(ϕ α3 + ).                (30)

Ay = Cy + Bx3 sinϕ3 + Ax2 sin(ϕ α3 + )+l2 cos(ϕ α3 + )

Выражения (30) легко приводятся к линейной системе двух уравнений, решение которых мы проведем по правилу Крамера

b1       a12                                      a11      b1

                                          B_x3 = _a^b11^{2                                               a}_a²²12       A_x2 = _a^a11²¹ _a^b1²2 ,                                      (31)

a21      a22                                    a21       a22

где коэффициенты      a₁₁,a₁₂,a₂₁,a₂₂,b₁,b₂ определяются        по        следующим зависимостям:

aa1121 == cossinϕϕ33       aa1222 == cossin((ϕ αϕ α33 ++ ))       bb12 == AAxy −−CCxy+−l al a2 222 12.                 (32)