



Курс «Численные методы».
Лабораторная работа №1
Нахождение математического ожидания и дисперсии случайной величины.
Цель работы
Необходимо построить датчик ПСЧ с равномерным законом распределения и найти математическое ожидание и дисперсию ПСЧ полученных с его помощью.
Для группы 07.19 допускается использование стандартного датчика ПСЧ Random.
Порядок нахождения математического ожидания и дисперсии СВ.
1. Интервал распределения случайной величины делим на несколько (для данной работы 15) равных подинтервалов. Длина каждого подитерваля находится как
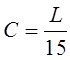 ,
,
где L - длина отрезка распределения.
2. Берем N случайных чисел, равномерно распределенных на отрезке [0..L], и подсчитываем количество случайных чисел A попавших в каждый подитервал.
3. Строим гистограмму распределения. Пример гистограммы для отрезка [0..1] (L=1) показан на рис 1.
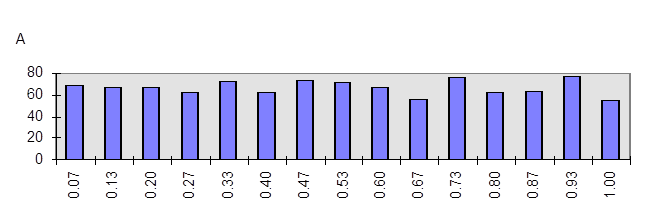
Рис. 1
4. Математическое ожидание находим по формуле
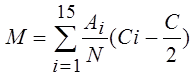 , где выражение
, где выражение 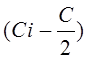 определяет
середину i-го подинтервала.
определяет
середину i-го подинтервала.
5. Дисперсию находим по формуле
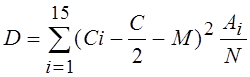
Задание
Для указанных в варианте условий найти математическое ожидание и дисперсию для случайной величины с равномерным законом распределения. Построить гистограмму распределения по подинтервалам в табличном процессоре Exсel.
Варианты
L - длина отрезка распределения
N - количество исследуемых чисел
|
Вар. |
L |
N |
Метод построения датчика |
Вар. |
L |
N |
Метод построения датчика |
|
1 |
10 |
200 |
Вычетов |
16 |
160 |
200 |
Вычетов |
|
2 |
20 |
200 |
Др. часть |
17 |
170 |
200 |
Др. часть |
|
3 |
30 |
200 |
Вычетов |
18 |
180 |
200 |
Вычетов |
|
4 |
40 |
200 |
Др. часть |
19 |
190 |
200 |
Др. часть |
|
5 |
50 |
200 |
Вычетов |
20 |
200 |
200 |
Вычетов |
|
6 |
60 |
200 |
Др. часть |
21 |
210 |
200 |
Др. часть |
|
7 |
70 |
200 |
Вычетов |
22 |
220 |
200 |
Вычетов |
|
8 |
80 |
200 |
Др. часть |
23 |
230 |
200 |
Др. часть |
|
9 |
90 |
200 |
Вычетов |
24 |
240 |
200 |
Вычетов |
|
10 |
100 |
200 |
Др. часть |
25 |
250 |
200 |
Др. часть |
|
11 |
110 |
200 |
Вычетов |
26 |
260 |
200 |
Вычетов |
|
12 |
120 |
200 |
Др. часть |
27 |
270 |
200 |
Др. часть |
|
13 |
130 |
200 |
Вычетов |
28 |
280 |
200 |
Вычетов |
|
14 |
140 |
200 |
Др. часть |
29 |
290 |
200 |
Др. часть |
|
15 |
150 |
200 |
Вычетов |
30 |
300 |
200 |
Вычетов |
Курс «Численные методы».
Лабораторная работа №2
Вычисление объема / площади фигур методом Монте Карло.
Для выполнения данной лабораторной работы необходимо запустить исполняемый файл lab2.exe. Далее следует выбрать фигуру указанную в Вашем варианте и установить ее геометрические размеры (рис 1.).
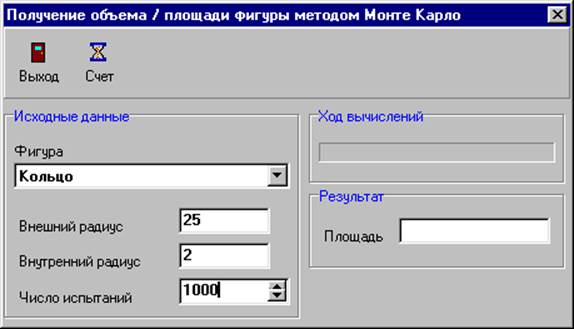
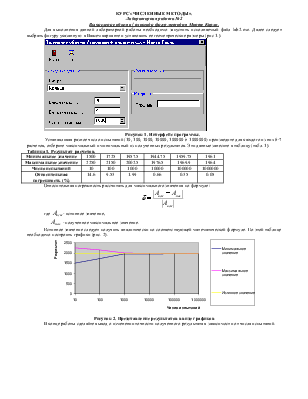
Рисунок 1. Интерфейс программы.
Устанавливая разное число испытаний (10, 100, 1000, 10000, 100000 è 1000000) произведите для каждого из них 6-7 расчетов, отберите максимальный и минимальный из полученных результатов. Эти данные занесите в таблицу (табл. 1).
Таблица 1. Результат расчетов.
|
Минимальное значение |
1500 |
1725 |
1957.5 |
1944.75 |
1959.75 |
1961 |
|
Максимальное значение |
2250 |
2150 |
2002.5 |
1976.5 |
1969.9 |
1964 |
|
Число испытаний |
10 |
100 |
1000 |
10000 |
100000 |
1000000 |
|
Относительная погрешность (%) |
14.6 |
9.53 |
1.99 |
0.66 |
0.35 |
0.05 |
Относительная погрешность рассчитать для максимального значения по формуле:
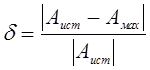
где ![]() -
истинное значение,
-
истинное значение,
![]() -
полученное максимальное значение.
-
полученное максимальное значение.
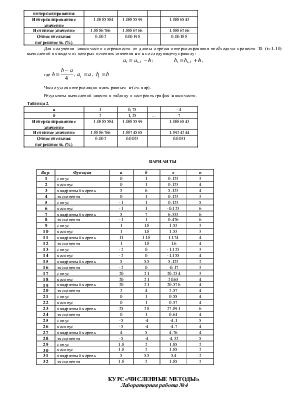
Истинное значение следует получить аналитически по соответствующей математической формуле. По этой таблице необходимо построить графики (рис. 2).
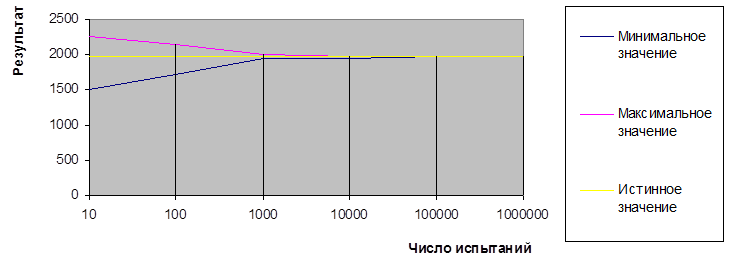
Рисунок 2. Представление результатов в виде графиков
В конце работы сделайте вывод о изменении точности полученного результата в зависимости от числа испытаний.
ФОРМУЛЫ ДЛЯ РАСЧЕТА ИСТИННОГО ЗНАЧЕНИЯ
Площадь
круга ![]()
Объем
цилиндра ![]()
Объем
шара 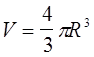
ВАРИАНТЫ
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.