Введение в теорию графов. Общие сведения. Первая граф-модель. Области применения теории графов. Классификация графов

Введение в теорию графов.

1.  Общие сведения.

Т.Г. – это математический язык для формализации определения понятий связанных с анализом и синтезом структур и объектов, систем и процессов.

Т.Г. – самостоятельный раздел дискретной математики, который включает алгебр. теорию графов, алгоритмическую т.г. (построение различных объектов на графе), прикладная теория графов (применение т.г. для решения конкретных задач).

Появилась новая дисциплина  – структурная информатика, которая возникла на стыке т.г., визуальном программировании и теории групп.

2.  Историческая справка.

Леонард Эйлер, 1736 год.

Задача о Кенигсбергских мостах.

? Можно ли обойти все участки суши по 1 разу и вернуться к исходной точке, пройдя 1 раз по одним мостам.

Первая граф-модель.

Задача об обходах графов.

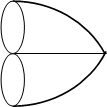             С                                    Т. необходимым и достаточным условием существования обходов   в графе является

                                                      его связность и четность степеней вершин.

А                            D                                     

B

 

Эйлеров  Эйлеров см. ниже.

граф,           путь

1936 год. Венгерский математик Кеник Д. “Теория конечных и бесконечных графов”, – книга.

3.  Области применения теории графов.

Химия. Химическая информатика.

Электротехника. Электроника.

Молекулярная биология (ДНК).

Психология. Социология.

Программирование, информатика и др.

Основные определения.

Опр.1.G=(X,U), X≠0, UXX, UX ²

      X – множество вершин графа,

U – множество ребер.

Пример. Задать все графы на 4 вершинах.

G=(X,U), где│X│=4

граф с изомер.

вершиной.

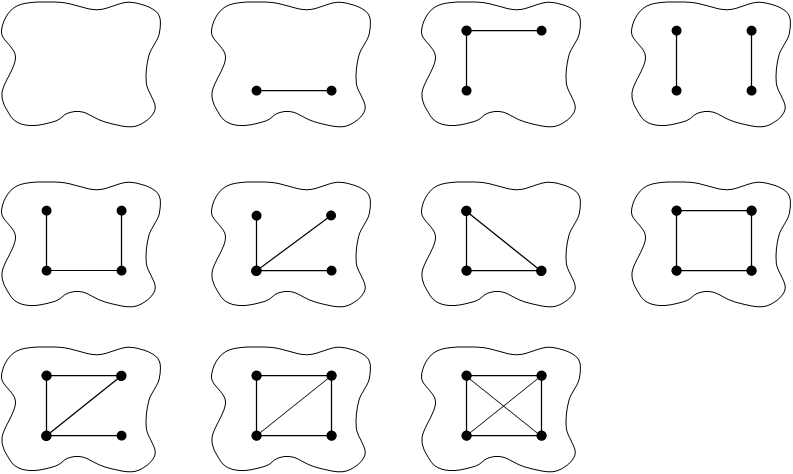
1                 2                               1                2              

3                4    

G₁(4,0)                                         G₂                                                               G₃                                                               G₄                             

G₅                                                                G₆                                                                G₇                                       G₈(?) цикл

G₉                                     G₁₀                                                      G₁₁

полный граф

1. Орграф.

 

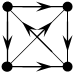
ребро с ориентацией – дуга.

2. Мультиграф.

                        

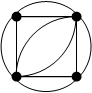
несколько ребер к одной вершине.

3. Псевдограф.

 

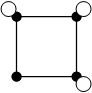если есть петли то псевдограф.

4.Несвязный граф(несвязанный).

                                                 несвязанный граф с компонентами связан к=3(элементов)

l

а

Рисунок 1.

q

c

b                                 e                

d

G(X,U), U?XX

Задавая граф множеством вершин и ребер, мы задаем “U” как способ отображения X в X.

U:XX U–отображения из “X” в “X”.

 Классификация графов.

Признак классификации	графы
1.Ориентация(может быть или нет)	–  орграф –  неорграф –  смешанный граф
2.Взвешенность: структурная или функциональная	–  взвешенный функцией –  невзвешенный граф –  частично взвешенный

Виды весов:                                                         Тип взвешемости: 

–арифметические числа                                      – реберная       

–функции                                                              – вершинная

–логические                                             – смешанный вариант

Основные характеристики графов.

1.   Число вершин n=│X│ – мощность множества вершин.

2.   Число ребер m=│U│ – мощность множества ребер.

граф: G (n, m)

3.Смежность вершин.

  1       U₁     2           Две вершины смежны, если они соединены ребром.

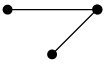                                Смежность ребер.

3      U₂           Два ребра называются смежными, если они имеют общую вершину.

4.Инцидентность

– вершины ребру: если ребро связано с данной вершиной. Например, ребро U.инцидентно вершине 1.

Степень вершины:

число ребер инцидентных одной вершине.

?(2)=2=│ГХ│

множество вершин смежных с вершиной 2.

Граф называется однородным (регулятивным), если степени всех вершин одинаковы (пример: граф G₁₁, G₁, G₄, G₈).

5.Для орграфа – множество предков и множество потомков.

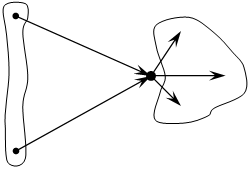
множество потомков х_i

??? x_i=│Г^–( x_i )│+│ Г( x_i )│

если Г^–1( x_i )= Ø и

Г( x_i )      Г( x_i )≠Ø то x_i – изолированная вершина

Множество предков Г^–(x_i)

Части графа.

G(X, U) –граф

I.  Подграф G^׀(X^׀, U^׀)/ X^׀?X, U^׀ содержит все те ребра графа G из U, которые инцидентны всем вершинам из множества X^׀.

II.  Частичный граф(суграф). G^׀׀(X,U^׀CU).

III.  Частичный подграф. G^׀׀׀(X^׀CX_____U^׀CU).

Пример

G(X,U)

 

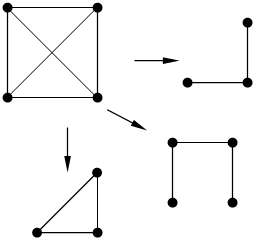G′′′

III

G′

G″

II

I

Пути на графике.

Орграф                                  неорграф

Дуга                                      ребро

Путь – совокупность дуг,                              цепь определяющий путь из одной вершины в другую.

Контур                                                         цикл

Граф называется связанным, если любые вершины можно соединить цепью.

Граф называется вязанным, если его можно разбить на подгруппы, что все вершины в каждом подграфе связаны, а вершины из различных подграфов не связаны. См. рисунок 1. Частным случаем связанного неориентированного графа с min числом дуг, является дерево.

 

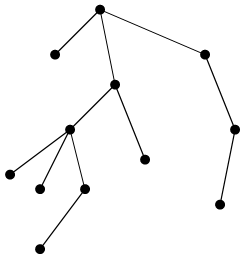Дерево.

Характеризуется тем, что между двумя любыми вершинами существует точно 1 путь из x_i в x_j.

G(n,n-1)

Длина пути.

Длиной пути μ(x_i,x_j) называется число, равное числу дуг, составляющих данный путь (если дуги не взвешены), и равные числу сумм весов дуг, составляющих данный путь.

1                     2

 

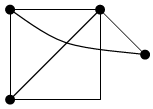                                   3           μ(3,5)=2(минимальное кол-во ребер).

5                    4

7

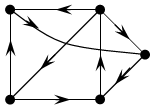                              1

5                          μ(3,5)=μ(3,2,5)=3

8      2                                μ(3,4,5)=3+4=7

3

4                                 Для орграфа важным является ориентация.

μ(3,5,2)=3+5+2=8

Матричная форма представления графа.

Существует 3 вида матриц для представления графов в ЭВМ.

1)  Матрица смежности.

А=║а_ij║_nn, где а_ij=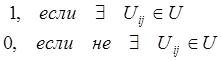      

Матрица А задает граф с точностью до изоморфизма(по структуре однозначно строится матрица).

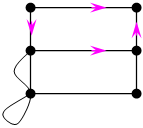                                   А₆₆=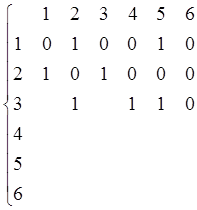

если граф ориентированный.

2) Матрица инцидентности.

S=║S_ij║_nm, гдеS=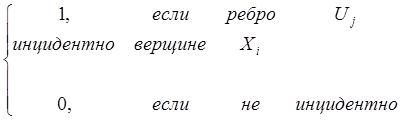

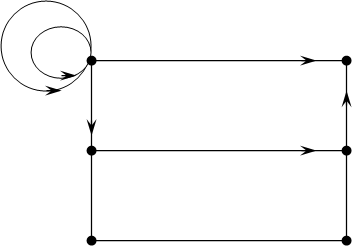
U₈ 1                           U₁                             2

                      

U₃

 

5                                                                 3

U₃

6                                                                       4

U₇

S₆₇=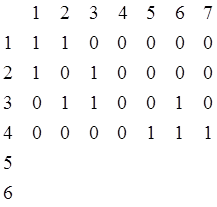

Для орграфа учитывается ориентация.

+1, если ребро выходит из вершины;

-1, если ребро заходит;

0, если не инцидентно;

сonst, если имеется петля (кол-во петель =const).

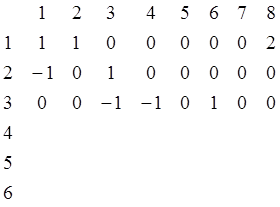
Матрица S задает граф с точностью до изомиорфизма, основное преимущество матрицы А перед матрицей S в том, что за один шаг алгоритма можно получить ответ на вопрос, есть ли ребро из вершины х_i в х_j.

Основной недостаток матрицы А – большой объем памяти независимо от ребер: n².

Домашнее задание!!!

1.изучить стр.10-13, проиллюстрировав каждое определение на графе.

2.стр.14-17 выучить матрицы, задание графа с помощью векторов., с.16-20(самостоятельно изучить).

Домашнее задание.

1.Проиллюстрировать определения графами.

1)Совокупность множества Х вершин и множества Е связей между ними называется графом и обозначается G=(X,E).

                                      x₁

                                                                   l₄                  G=(4,6)

l₂

                                 x₄

      x₂                                                   l₆

l₃                              x₂

l₅.

2)Если связь имеет направление, то она называется дугой, в противном случае – ребром.

                                                                                                                                 ребро l

дуга l

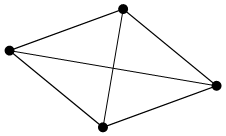
3)Граф, у которого все связи являются ребрами, называется неографом.

               U₄

U₆        U₁

U₅  

U₃                                U₂

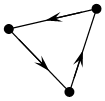
4)Граф с дугами называется ориентированным графом (орграфом).

U₃

 

U₂             U₁

5)Если у графа существуют кратные ребра, т.е. несколько ребер, соединяющих одну и туже пару вершин, то такие графы называются мультиграфами.

                                                                                    U₁

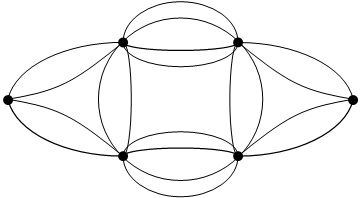
                        а                                  в                      U₂

                                                                                                                     мультиграф G=(6,20)

                                                                                               U₃

U₄

а, в – 2 вершины графа;

U₁,U₂,U₃,U₄ – кратные ребра, соединяющие вершины а и в.

6)Ребро оба конца которого связаны с одной и той же вершиной, называются петлей.

                                                   петля

Вершина

7)Граф называется псевдографом, если множество Е включает ребра, дуги, петли и все они могут быть кратными.

дуга U₉                                          дуга U₈                            петля U₁

 

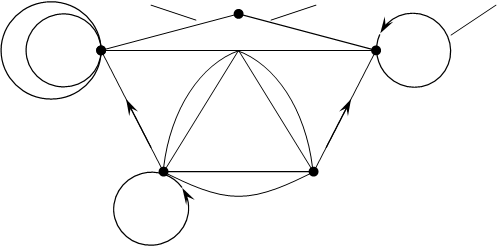                                                                   ребро U₅                               ребро U₆

 

                                                                                                                                                      дуга U₃

              петля U₆                                                                                                              дуга U₂                           

         петля U₇

                                                                                                                                       дуга U₄                                                                                                                                                                   кратные

                       ребро l₃                                     

                ребро l₄                                                                                  ребро l₂

                    петля U₅                                                                                ребро l₂                                               кратные    

8)Две вершины называются смежными, если они соединяются некоторым ребром (дугой) графа, и две различные дуги(ребра) смежны, если они имеют общую вершину.

a            U₁            b

 

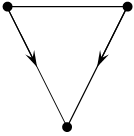U₃                           U₂

 

C

9)Вершина Х_i инцидентна дуге (ребру) е_ij, если она является началом или концом дуги(ребра).

1                   e_{12                            2}

 

Х₁ инцидентна дуге е₁₂, т.к. Х₁ начало е₁₂.

Х₂ инцидентна дуге е₁₂, т.к. Х₂ конец е₁₂.

10)Дуга(ребро) е_ij инцидентна вершине Х_i, если она выходдит из этой вершины.

                  x₁

l₁₂ инцидентна Х_i+

e₁₂

11)Число ребер (дуг), инцидентных некоторой вершине х₁, называют степенью вершины.

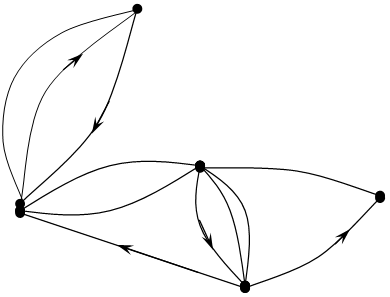                                                                  x₅

e₁₁

e₁₀

e₉

e₇                    x₁            e₅

e₈                                                                           x₄

e₂    e₁

e₆

e₄

x₂

Например степень вершины: Х₁:6;

(ребра е₇, е₈, е₂, е₁, е₅, дуга е₇) степень вершины X₅:3;

(ребро e₁₁, дуга e₇ и т.д.)

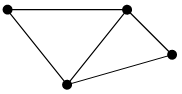
12)Для неографа сумма степеней вершин равна удвоенному числу его ребер.

x₁                   U₁    x₂                                            Ст. свободы x₁ : 2

                                                               Ст. свободы x₂ : 3

U₄               U₂                            Ст. свободы x₃ : 2

U₅                                        x₃                   Ст. свободы x₄ : 3

U₃

x₄      Неорграф G=(4,5)

Сумма степеней свободы: S=2+3+2+3=10. Количество ребер n=5(U₁, U₂, U₃, U₄, U₅). S=2n=2∙5=10.

13)Для орграфа вводится понятие полустепени исхода и полустепени