Линейная экстраполяция. Коэффициент корреляции. Экстраполированное значение. Основное окно программы линейной экстраполяции

Лабораторная работа №1

Линейная экстраполяция

курс “Численные методы”часть вторая

Теоретический раздел.

Линейная экстраполяция это частный случай метода наименьших квадратов, в котором в качестве аппроксимирующей функции взята прямая.

Линейная экстраполяция возможна когда исследуемая величина имеет зависимость близкую к линейной, в противном случае экстраполяция невозможна.

Для того, что бы определить насколько линейна зависимость величин в заданном динамическом ряде используют коэффициент корреляции(r^*_n)· . Пусть имеем следующий динамический ряд, представляющий зависимость исследуемой величины X от текущего времени T:

Тогда коэффициент корреляции определяется как:

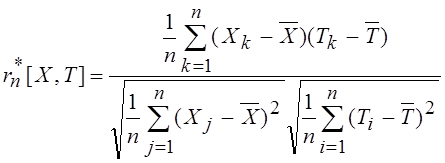,                         (1)

где  и  соответствующие средние значения:

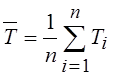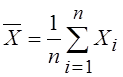,                          .                       (2)

Коэффициент корреляции представляет собой безразмерную величину и лежит в диапазоне [-1,1]. В случае когда он приближается к 1 имеем положительную линейную зависимость (рис. 1). Когда он приближается к -1 имеем отрицательную линейную зависимость.

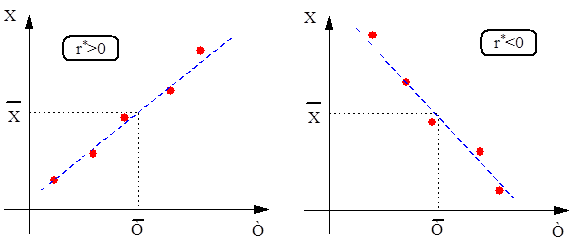
Рис. 1

Вообще, зависимость будет близка к линейной, если значение коэффициента по модулю не менее 0.75.

Если значение коэффициента корреляции по модулю превышает 0.75, то можно применять линейную экстраполяцию. При этом интерполирующая функция (прямая) имеет уравнение :

.                                                    (3)

Для того, что бы  получить экстраполированное значение  для момента времени  необходимо вычислить:

.                                          (4)

Однако значения коэффициентов k и b в этом выражении нам неизвестно. Эти коэффициенты определяют расположение нашей прямой и их необходимо выбрать таким образом, что бы прямая проходила как можно ближе к заданным значениям динамического ряда.

Для оценки этого используют параметр D, называемый квадратичной невязкой. Для случая линейной экстраполяции он рассчитывается как:

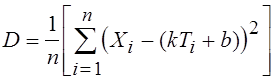.                                 (5)

Значение квадратичной невязки может лежать в диапазоне []. Чем меньше это значение, тем ближе прямая проходит к заданным точкам. Нулевое значение соответствует идеальному случаю, когда прямая проходит точно через все заданные точки.

Таким образом, коэффициенты k и b следует подбирать таким образом, чтобы получить минимальное значение квадратичной невязки. В этом случае мы можем ожидать наиболее точное экстраполированное значение .

Порядок выполнения работы.

Для начала запустите исполняемый файлlab1.exe.На экране появится основное окно программы (рис. 2).

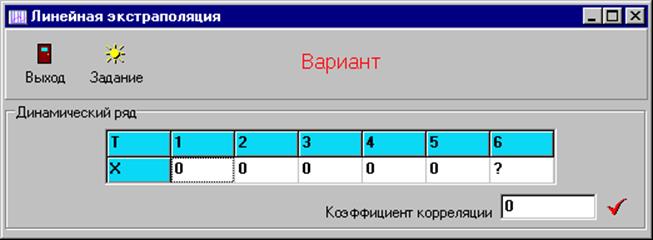
Рис. 2. Основное окно программы линейной экстраполяции.

Нажмите на кнопку Задание. В появившемся окне (рис. 3) наберите свой вариант и выберите номер задания (Вариант как и раньше определяется номером в списке по журналу. Все вопросы по наличию журнала следует адресовать старосте группы). В каждом варианте необходимо по очереди выполнить  все три задания.

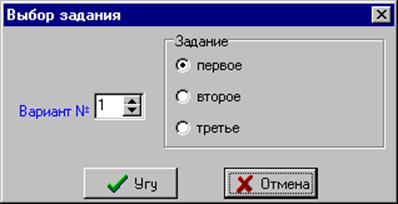
Рис. 3. Окно выбора варианта и задания.

После того как вы нажмете кнопку Угу программа сформирует динамический ряд для Вашего варианта и выбранного задания.

Пользуясь формулами (1) и (2) вычислите значения коэффициента корреляции с точностью до 0.01 и занесите его в соответствующее поле основного окна программы. Если после этого при нажатии кнопки  в основном окне появятся дополнительные элементы (рис. 4), то значение коэффициента определено верно. Если коэффициент определен неверно, то рассчитайте его заново. При значении коэффициента по модулю менее 0.75, линейная экстраполяция будет слишком грубой и в этом случае ее использовать не следует.

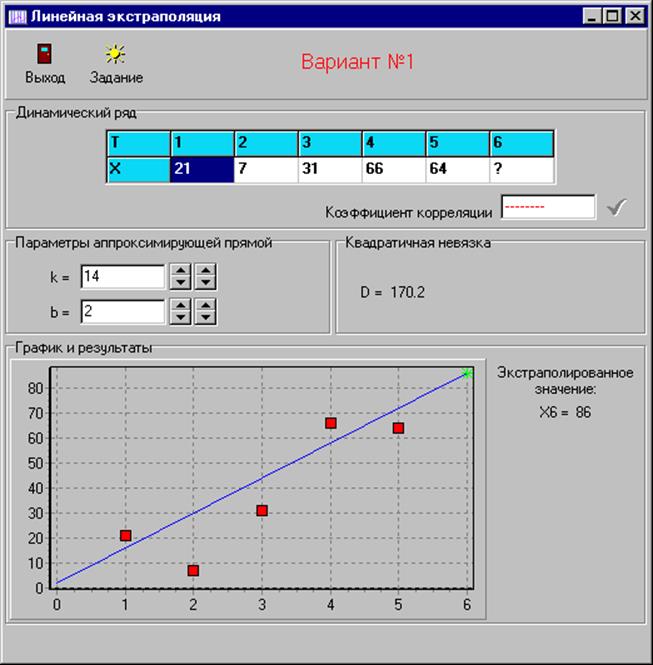
Рис. 4. Основное окно программы после расчета коэффициента корреляции.

Если коэффициент корреляции позволяет проводить линейную экстраполяцию, то необходимо изменяя коэффициентыkиbдобиться минимального значения квадратичной невязкиD. Изменение коэффициентов осуществляется при помощи кнопок .

Итак, для каждого из задания Вашего варианта необходимо получить:

1. Значение коэффициента корреляции

2. Значения k, b, D, Y₆ (если возможна линейная экстраполяция)

Советы по выполнению работы:

1. В каждом варианте только одно задание не позволяет производить линейную экстраполяцию.

2. Не надо пытаться подбирать коэффициент корреляции. Быстрее и проще его рассчитать (все равно расчет буду спрашивать).

3. Поиск у соседей динамического ряда похожего на Ваш пустая трата времени. Задания в вариантах не повторяются.